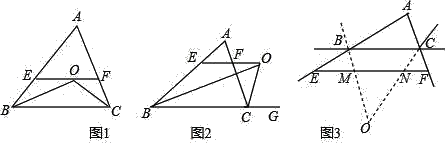
题目内容
【题目】如图，在
中，
，
为
边的中点，
为等边三角形.
（1）求证：
；
（2）若
，在
边上找一点
，使得
最小，并求出这个最小值.
【答案】（1）证明见解析；（2）
的最小值为3.
【解析】
（1）根据直角三角形的性质可得：
，然后根据等边三角形的性质可得：
，从而得出
，然后利用SAS即可证出：
.
（2）作点
关于直线
的对称点
，连接
交于点
，根据两点之间线段最短，此时
最小，为的长，则最小，为
. 则点H即为所求，然后根据等边三角形的判定可证出
为等边三角形，从而得出
是直角三角形，最后根据勾股定理，即可求出的最小值.
（1）证明：在
中，
，为
边的中点，
∴.
∵
为等边三角形，
∴.
∴
.
∴.
在△ADE和△CDB中
∴
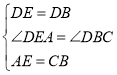
（2）如图，作点关于直线的对称点，连接交于点，
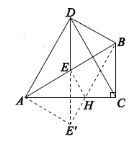
根据两点之间线段最短，此时最小，为的长，
则最小，为. 则点H即为所求.
在中，
，
∴
，则
.
∴∠
∠EAC=60°
∴为等边三角形
∴
∴是直角三角形
∴
.
∴的最小值为3
练习册系列答案
相关题目
