题目内容
【题目】为弘扬中华传统文化,某校组织八年级![]() 名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为
名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为![]() 分)进行统计分析,得到如下所示的频数分布表:
分)进行统计分析,得到如下所示的频数分布表:
分数段 |
|
|
|
|
|
频数 |
|
|
|
|
|
所占百分比 |
|
|
|
|
|

请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查的样本容量为___ _,表中![]() _ ,
_ ,![]() _;
_;
(2)补全如图所示的频数分布直方图;
(3)若成绩超过![]() 分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?
分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?
【答案】(1)200、80、12;(2)见详解(3)该校八年级学生中汉字听写能力优秀的约有4160人.
【解析】
(1)根据第一组的频数是16,频率是0.08,即可求得总数,即样本容量;
(2)根据(1)的计算结果即可作出直方图;
(3)利用总数8000乘以优秀的所占的频率即可.
解:(1)样本容量是:16÷0.08=200;
样本中成绩的中位数落在第四组;
m=200×0.40=80,![]() =
=![]() =0.12,则n=12
=0.12,则n=12
故答案为:200、80、12;
(2)补全频数分布直方图,如下: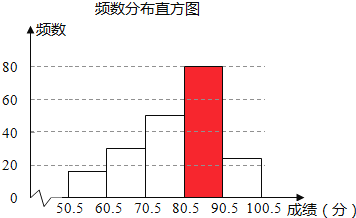
(3)8000×(0.4+0.12)=4160(人).
答:该校八年级学生中汉字听写能力优秀的约有4160人.

 走进文言文系列答案
走进文言文系列答案【题目】某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,(即出厂价=基础价+浮动价)其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据,已知出厂一张边长为40cm的薄板,获得利润是26元.(利润=出厂价-成本价)
薄板的边长(cm) | 20 | 30 |
出厂价(元/张) | 50 | 70 |
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值。




