题目内容
【题目】如图,在平面直角坐标系中,△ABO的面积为8,OA=OB,BC=12,点P的坐标是(a,6).
(1) △ABC三个顶点的坐标分别为A( , ),B( , ),C( , );
(2) 是否存在点P,使得![]() ?若存在,求出满足条件的所有点P的坐标.
?若存在,求出满足条件的所有点P的坐标.

【答案】(1)A(0,4),B(-4,0),C(8,0); (2)点P的坐标为(14,6)或(-10,6).
【解析】
(1)根据三角形面积公式得到![]() OA2=8,解得OA=4,则OB=OA=4,OC=BCOB=8,然后根据坐标轴上点的坐标特征写出△ABC三个顶点的坐标;
OA2=8,解得OA=4,则OB=OA=4,OC=BCOB=8,然后根据坐标轴上点的坐标特征写出△ABC三个顶点的坐标;
(2)先计算出S△ABC=24,再根据(2)中的分类得到2a4=24或42a=24,然后分别求出a的值,从而确定P点坐标.
(1)∵S△ABO=![]() OAOB,
OAOB,
而OA=OB,∴![]() OA2=8,解得OA=4,
OA2=8,解得OA=4,
∴OB=OA=4,
∴OC=BCOB=124=8,
A(0,4),B(-4,0),C(8,0);
(2)解:![]() .
.
当点P在第一象限,即a>0时,作PH⊥x轴于H,如图①.

图①
![]() .
.
则2a-4=24. 解得a=14.此时点P的坐标为(14,6).
当点P在第二象限,即a<0时,作PH⊥y轴于H,如图②.
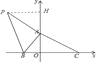
图②
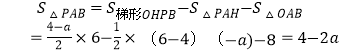
则4-2a=24. 解得a=-10.此时点P的坐标为(-10,6).
综上所述,点P的坐标为(14,6)或(-10,6).

【题目】为弘扬中华传统文化,某校组织八年级![]() 名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为
名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为![]() 分)进行统计分析,得到如下所示的频数分布表:
分)进行统计分析,得到如下所示的频数分布表:
分数段 |
|
|
|
|
|
频数 |
|
|
|
|
|
所占百分比 |
|
|
|
|
|

请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查的样本容量为___ _,表中![]() _ ,
_ ,![]() _;
_;
(2)补全如图所示的频数分布直方图;
(3)若成绩超过![]() 分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?
分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?




