题目内容
【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2![]() ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.


(Ⅰ)如图1,求∠DAO的大小及线段DE的长;
(Ⅱ)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3![]() .
.
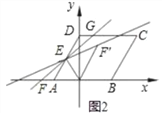
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
【答案】(Ⅰ)∠DAO=60°,DE=2; (Ⅱ)①GH=6,DG=﹣3+![]() ;②F(﹣5﹣
;②F(﹣5﹣![]() ,0).
,0).
【解析】解:(Ⅰ)∵A(﹣2,0),D(0,2![]() )∴AO=2,DO=2
)∴AO=2,DO=2![]() ,∴tan∠DAO=
,∴tan∠DAO=![]() =
=![]() ,
,
∴∠DAO=60°,∴∠ADO=30°,∴AD=2AO=4,∵点E为线段AD中点,∴DE=2;
(Ⅱ)①如图2,

过点E作EM⊥CD,∴CD∥AB,∴∠EDM=∠DAB=60°,∴EM=DEsin60°=![]() ,∴GH=6,
,∴GH=6,
∵CD∥AB,∴∠DGE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,∴△OEF′≌△OEF,∴∠OFE=∠OF′E,
∵点E是AD的中点,∴OE=![]() AD=AE,
AD=AE,
∵∠EAO=60°,∴△EAO是等边三角形,∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,∴∠EOF′=∠EOA=60°,
∴∠EOF′=∠AEO,∴AD∥OF′,∴∠OF′E=∠DEH,∴∠DEH=∠DGE,
∵∠DEH=∠EDG,∴△DHE∽△DEG,∴![]() ,∴DE2=DG×DH,
,∴DE2=DG×DH,
设DG=x,则DH=x+6,∴4=x(x+6),∴x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ,∴DG=﹣3+
,∴DG=﹣3+![]() .
.
②如图3,

过点E作EM⊥CD,∴CD∥AB,∴∠EDM=∠DAB=60°,∴EM=DEsin60°=![]() ,∴GH=6,
,∴GH=6,
∵CD∥AB,∴∠DHE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,∴△OEF′≌△OEF,∴∠OFE=∠OF′E,
∵点E是AD的中点,∴OE=![]() AD=AE,
AD=AE,
∵∠EAO=60°,∴△EAO是等边三角形,∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,∴∠EOF′=∠EOA=60°,∴∠EOF′=∠AEO,∴AD∥OF′,
∴∠OF′E=∠DEH,∴∠DEG=∠DHE,
∵∠DEG=∠EDH,∴△DGE∽△DEH,∴![]() ,∴DE2=DG×DH,
,∴DE2=DG×DH,
设DH=x,则DG=x+6,∴4=x(x+6),∴x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ,
,
∴DH=﹣3+![]() .∴DG=3+
.∴DG=3+![]() ∴DG=AF=3+
∴DG=AF=3+![]() ,∴OF=5+
,∴OF=5+![]() ,∴F(﹣5﹣
,∴F(﹣5﹣![]() ,0).
,0).




