题目内容
【题目】在□ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE.
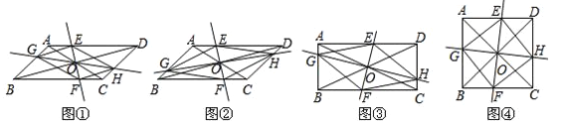
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
【答案】(1)四边形EGFH是平行四边形;(2)菱形;(3)菱形;(4)四边形EGFH是正方形.
【解析】
试题分析:(1)由于平行四边形对角线的交点是它的对称中心,即可得出OE=OF、OG=OH;根据对角线互相平分的四边形是平行四边形即可判断出EGFH的性质;
(2)当EF⊥GH时,平行四边形EGFH的对角线互相垂直平分,故四边形EGFH是菱形;
(3)当AC=BD时,对四边形EGFH的形状不会产生影响,故结论同(2);
(4)当AC=BD且AC⊥BD时,四边形ABCD是正方形,则对角线相等且互相垂直平分;可通过证△BOG≌△COF,得OG=OF,从而证得菱形的对角线相等,根据对角线相等的菱形是正方形即可判断出EGFH的形状.
试题解析:(1)四边形EGFH是平行四边形;
证明:∵ABCD的对角线AC、BD交于点O
∴点O是ABCD的对称中心;
∴EO=FO,GO=HO;
∴四边形EGFH是平行四边形;
(2)∵四边形EGFH是平行四边形,EF⊥GH,
∴四边形EGFH是菱形;
(3)菱形;
由(2)知四边形EGFH是菱形,
当AC=BD时,对四边形EGFH的形状不会产生影响;
(4)四边形EGFH是正方形;
证明:∵AC=BD,
∴ABCD是矩形;
又∵AC⊥BD,
∴ABCD是正方形,
∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;
∵EF⊥GH,
∴∠GOF=90°;
∠BOG+∠BOF=∠COF+∠BOF=90°
∴∠BOG=∠COF;
∴△BOG≌△COF(ASA);
∴OG=OF,同理可得:EO=OH,
∴GH=EF;
由(3)知四边形EGFH是菱形,
又EF=GH,
∴四边形EGFH是正方形.

 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】一元二次方程2x2﹣3x-1=0的二次项系数a、一次项系数b和常数c分别是( )
A.a=2,b=3,c=-1B.a=2,b=1,c=3
C.a=2,b=﹣3,c=﹣1D.a=2,b=﹣3,c=1
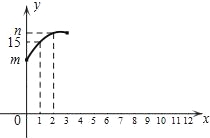
【题目】为进一步缓解城市交通压力,湖州推出公共自行车.公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
时段 | x | 还车数 | 借车数 | 存量y |
7:00﹣8:00 | 1 | 7 | 5 | 15 |
8:00﹣9:00 | 2 | 8 | 7 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:
(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知10:00﹣11:00这个时段的还车数比借车数的2倍少4,求此时段的借车数.