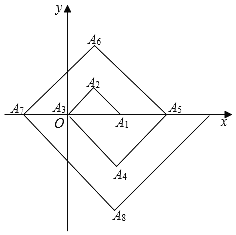
题目内容
【题目】在平面直角坐标系xOy中,图形W在坐标轴上的投影长度定义如下:
设点P![]() ,Q
,Q![]() 是图形W上的任意两点.若
是图形W上的任意两点.若![]() 的最大值为m,则图形W在x轴上的投影长度
的最大值为m,则图形W在x轴上的投影长度![]() =m;若
=m;若![]() 的最大值为n,则图形W在y轴上的投影长度
的最大值为n,则图形W在y轴上的投影长度![]() =n,如下图,图形W在x轴上的投影长度
=n,如下图,图形W在x轴上的投影长度![]() =
=![]() =2;在y轴上的投影长度
=2;在y轴上的投影长度![]() =
=![]() =4.
=4.
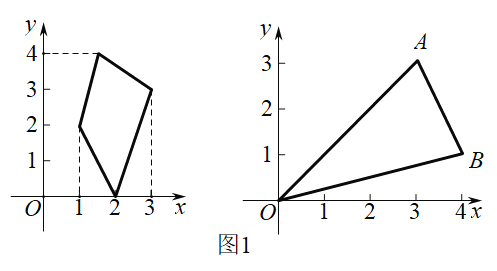
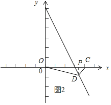
(1)已知点A(3,3),B(4,1).如图1所示,若图形W为△OAB,则![]() =___________
=___________ ![]() =___________
=___________
(2)已知点C(4,0),点D在直线y=-2x+6上,若图形W为△OCD.当=![]() 时,求点D的坐标.
时,求点D的坐标.
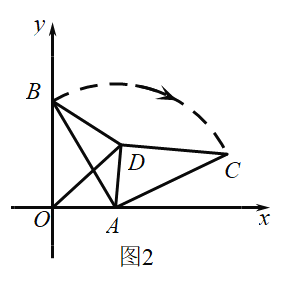
(3)如图2所示,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD,BD.若图形W为点O.A.C.D.B围成的多边形图象,且∠DOA=∠OBA,直接写出![]() 的值
的值
【答案】(1)![]() ;(2)点D的坐标为(1,4)或(6,-6),(3)
;(2)点D的坐标为(1,4)或(6,-6),(3)![]() 或
或![]()
【解析】
(1)确定出点A在y轴的投影的坐标、点B在x轴上投影的坐标,于是可求得问题的答案;
(2)过点P作PD⊥x轴,垂足为P.设D(x,-2x+6),则PD=|-2x+6|.PC=|4-x|,然后依据![]() ,列方程求解即可.
,列方程求解即可.
(3)分情况讨论,当D在第一象限时,由旋转的性质结合∠DOA=∠OBA,证明![]() 三点共线,过C作CF
三点共线,过C作CF![]() OB于F,过C作CG
OB于F,过C作CG![]() OA于G,设
OA于G,设![]() 利用勾股定理列出方程组即可得到答案.当D在第四象限时,过D作DF
利用勾股定理列出方程组即可得到答案.当D在第四象限时,过D作DF![]() OB于F,过D作DG
OB于F,过D作DG![]() OA于G,则四边形
OA于G,则四边形![]() 为矩形,设
为矩形,设![]() 建立方程组求解即可.
建立方程组求解即可.
解:(1)∵A(3,3),
∴点A在y轴上的正投影的坐标为(0,3).
∴△OAB在y轴上的投影长度![]() .
.
∵B(4,1),
∴点B在x轴上的正投影的坐标为(4,0).
∴△OAB在x轴上的投影长度![]() .
.
故答案为:4,3.
(2)如图1所示;过点P作PD⊥x轴,垂足为P.
0≤x≤3时,-2x+6=4, 解得x=1.
∴D(1,4).
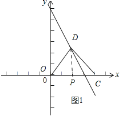
如图2所示:过点D作DP⊥x轴,垂足为P.
当3<x≤4时,
所以2x-6=4,
解得:x=5(舍去),
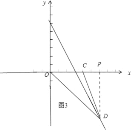
如图3所示,当点D在C点右侧,x>4时,
x=2x-6, 可得x=6 ,
点D坐标(6,-6),
如图4所示:当 x<0时,-2x+6=4-x,
解得:x=2 舍去,
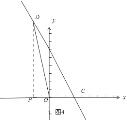
综上所述,点D的坐标为(1,4)或(6,-6).
(3)如图,当D在第一象限时,
![]() ∠DOA=∠OBA,
∠DOA=∠OBA,
![]()
![]()
![]()
由旋转可知:![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]()
![]() 三点共线,
三点共线,![]()
过C作CF![]() OB于F,过C作CG
OB于F,过C作CG![]() OA于G,
OA于G,
则四边形![]() 为矩形,
为矩形,
设![]()
![]()
![]()
![]()
由勾股定理得:
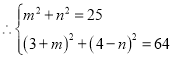
消去![]() 得:
得:![]()
![]()
![]() (舍去)
(舍去)
![]()
![]()
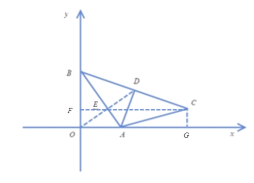
如下图,当点C旋转到![]() 轴的负半轴上,D在第四象限时,
轴的负半轴上,D在第四象限时,
![]()
![]()
同理可得:![]() 是
是![]() 的垂直平分线,
的垂直平分线,
过D作DF![]() OB于F,过D作DG
OB于F,过D作DG![]() OA于G,
OA于G,
则四边形![]() 为矩形,
为矩形,
设![]()
同理可得:
消去![]() 得:
得:![]()
![]()
![]() (舍去)
(舍去)
![]()
此时:![]()
综上:![]() 或
或![]()

【题目】好邻居超市购进一批面粉,标准质量为![]() ,现抽取
,现抽取![]() 袋样品进行称重检测,为记录的方便,用“
袋样品进行称重检测,为记录的方便,用“![]() ”表示超过标准的重量,用“
”表示超过标准的重量,用“![]() ”表示不足标准的重量,结果如下表(单位
”表示不足标准的重量,结果如下表(单位![]() ):
):
与标准差( |
|
|
|
|
|
|
|
|
袋数 |
|
|
|
|
|
|
| 3 |
(1)求这![]() 袋样品超出或不足的质量为多少?
袋样品超出或不足的质量为多少?
(2)这批面粉的总重量为多少千克?