题目内容
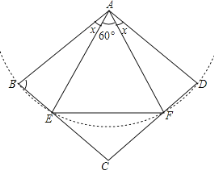
【题目】如图所示,已知AB∥CD,AB=CD,∠A=∠D.
(1)求证:四边形ABCD为矩形
(2)若点E是AB边上的中点,点F为AD边上一点,∠1=2∠2,CF=5,求AF+BC的值

【答案】(1)见详解;(2)5.
【解析】
(1)由题意根据矩形的判定定理即“有一内角为直角的平行四边形是矩形”进行证明即可;
(2)根据题意延长DA,CE交于点G,并运用全等三角形的判定和性质以及等腰三角形的性质进行综合分析即可求解.
解:(1)证明:∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵AB∥CD,
∴∠A+∠D=180°,
又∵∠A=∠D,
∴∠A=∠D=90°,
∴四边形ABCD为矩形;
(2)延长DA,CE交于点G,
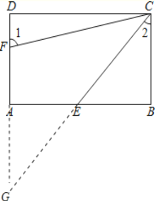
∵四边形ABCD是矩形,
∴∠DAB=∠B=90°,AD∥BC,
∴∠GAE=90°,∠G=∠2,
∵E是AB边的中点,
∴AE=BE,
在△AGE和△BCE中,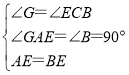 ,
,
∴△AGE≌△BCE(AAS),
∴AG=BC,
∴![]() ,
,
∵∠1=2∠2=![]() ,∠G=∠2,
,∠G=∠2,
∴![]() ,
,
∵CF=5,
∴AF+BC=5.

练习册系列答案
相关题目