题目内容
【题目】如图,直线y= ![]() x+1与y轴交于A点,过点A的抛物线y=﹣
x+1与y轴交于A点,过点A的抛物线y=﹣ ![]() x2+bx+c与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
x2+bx+c与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).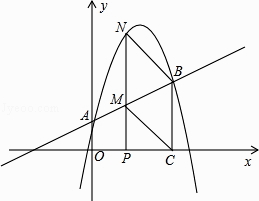
(1)直接写出抛物线的解析式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
【答案】
(1)
解:∵BC⊥x轴,垂足为点C,C(3,0),
∴B的横坐标为3.
将x=3代入y= ![]() x+1得:y=
x+1得:y= ![]() .
.
∴B(3, ![]() ).
).
将x=0代入y= ![]() x+1得:y=1.
x+1得:y=1.
∴A(0,1).
将点A和点B的坐标代入得: 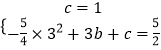 ,解得:b=
,解得:b= ![]() ,c=1.
,c=1.
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+1
x+1
(2)
解:设点P的坐标为(t,0),则N(t,﹣ ![]() t2+
t2+ ![]() t+1),M(t,
t+1),M(t, ![]() t+1).
t+1).
∴S=(﹣ ![]() t2+
t2+ ![]() t+1)﹣(
t+1)﹣( ![]() t+1)=﹣
t+1)=﹣ ![]() t2+
t2+ ![]() t.(0<t<3).
t.(0<t<3).
(3)
解:∵MN∥BC,
∴当MN=NB时,四边形BCMN为平行四边形.
∴﹣ ![]() t2+
t2+ ![]() t=
t= ![]() ,解得t=1或t=2.
,解得t=1或t=2.
∴当t=1或t=2时,四边形BCMN为平行四边形.
当t=1时,M(1, ![]() ).
).
依据两点间的距离公式可知:MC= ![]() =
= ![]() .
.
∴MN=MC.
∴四边形BCMN为菱形.
当t=2时,M(2,2),则MC= ![]() =
= ![]() .
.
∴MC≠MN.
∴此时四边形BCMN不是菱形.
综上所述,当t=1时,四边形BCMN为菱形
【解析】(1)先求得点B和点A的坐标,然后将原点坐标,点A和点B的坐标代入抛物线的解析式求解即可;(2)设点P的坐标为(t,0),则N(t,﹣ ![]() t2+
t2+ ![]() t+1),M(t,
t+1),M(t, ![]() t+1),然后依据MN等于M、N两点的纵坐标之差可得到S与t的函数关系式;(3)已知MN∥BC,故此当MN=NB时,四边形BCMN为平行四边形,然后列出方程组求解即可;当MC=MN时,四边形BCMN为菱形,然后分别将t=1和t=2代入求得点M的坐标,然后再求得MC的长,最后依据MC于是等于MN进行判断即可.
t+1),然后依据MN等于M、N两点的纵坐标之差可得到S与t的函数关系式;(3)已知MN∥BC,故此当MN=NB时,四边形BCMN为平行四边形,然后列出方程组求解即可;当MC=MN时,四边形BCMN为菱形,然后分别将t=1和t=2代入求得点M的坐标,然后再求得MC的长,最后依据MC于是等于MN进行判断即可.