题目内容
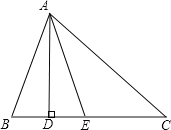
【题目】如图,在△ABC中,∠B>∠C,AD⊥BC,垂足为D,AE平分∠BAC.已知∠B=65°,∠DAE=20°,求∠C的度数.
【答案】25°
【解析】
试题分析:由垂直的定义得到∠ADB=90°,根据三角形的内角和得到∠BAD=90°﹣65°=25°,求得∠BAE=∠BAD+∠DAE=25°+20°=45°,根据角平分线的定义得到∠BAC=2∠BAE=2×45°=90°,根据三角形的内角和即可得到结论.
解:∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣65°=25°,
∴∠BAE=∠BAD+∠DAE=25°+20°=45°,
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2×45°=90°,
∴∠C=180°﹣∠B﹣∠BAC=25°.

【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
【题目】我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元. 经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元) | … | 70 | 90 | … |
销售量y(件) | … | 3000 | 1000 | … |
(利润=(售价﹣成本价)×销售量)
(1)求销售量y(件)与售价x(元)之间的函数关系式;
(2)你认为如何定价才能使工艺品厂每天获得的利润为40000元?