题目内容
如图在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.

(1)求∠DAC的度数.
(2)试说明DC=AB.
【答案】
(1)解:∵AB=AC,
∴∠B=∠C=30°,
∵∠C+∠BAC+∠B=180°,
∴∠BAC=180°-30°-30°=120°,
∵∠DAB=45°,
∴∠DAC=∠BAC-∠DAB=120°-45°=75°;
(2)证明:∵∠DAB=45°,
∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,
∴DC=AC,
∴DC=AB.
【解析】(1)由AB=AC,根据等腰三角形的两底角相等得到∠B=∠C=30°,再根据三角形的内角和定理可计算出∠BAC=120°,而∠DAB=45°,则∠DAC=∠BAC-∠DAB=120°-45°;
(2)根据三角形外角性质和得到∠ADC=∠B+∠DAB=75°,而由(1)得到∠DAC=75°,再根据等腰三角形的判定可得DC=AC,这样即可得到结论.

练习册系列答案
相关题目

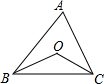 如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为
如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为 如图在△ABC中,∠A=45°,tanB=3,BC=
如图在△ABC中,∠A=45°,tanB=3,BC= 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE, 如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是
如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是