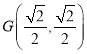Question

【题目】如图，把置于平面直角坐标系中，点A的坐标为，点B的坐标为，点P是内切圆的圆心．将沿x轴的正方向作无滑动滚动，使它的三边依次与x轴重合，第一次滚动后圆心为，第二次滚动后圆心为，…，依此规律，第2019次滚动后，内切圆的圆心的坐标是________．

Answer 1

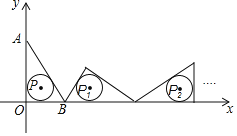
【答案】

【解析】

由勾股定理得出AB＝，求出Rt△OAB内切圆的半径＝1，因此P的坐标为（1，1），由题意得出P3的坐标（3＋5＋4＋1，1），得出规律：每滚动3次为一个循环，由2019÷3＝673，即可得出结果．

解：∵点A的坐标为（0，4），点B的坐标为（3，0），

∴OA＝4，OB＝3，

∴AB＝，

∴Rt△OAB内切圆的半径＝，

∴P的坐标为（1，1），

∵将Rt△OAB沿x轴的正方向作无滑动滚动，使它的三边依次与x轴重合，第一次滚动后圆心为P1，第二次滚动后圆心为P2，…，

∴P3（3＋5＋4＋1，1），即（13，1），每滚动3次为一个循环，

∵2019÷3＝673，

∴第2019次滚动后，Rt△OAB内切圆的圆心P2019的横坐标是673×（3＋5＋4）＋1，即P2019的横坐标是8077，

∴P2019的坐标是（8077，1）；

故答案为：（8077，1）．