题目内容
先将一矩形ABCD置于直角坐标系中,使点A与坐标系的原点重合,边AB,AD分别落在x轴、y轴上(如图1),再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图2),若AB=4,BC=3,则图1和图2中点B点的坐标为________,点C的坐标________.

(4,0),(2 ,2) (4,3)(
,2) (4,3)(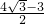 ,
,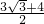 )
)
分析:根据旋转的性质求解.
旋转的性质是旋转不改变图形的大小和形状.
解答:∵AB=4,在x轴正半轴上,
∴图1中B坐标为(4,0),
在图2中过B作BE⊥x轴于点E,那么OE=4×cos30°=2 ,BE=2,
,BE=2,
在图2中B点的坐标为(2 ,2);
,2);
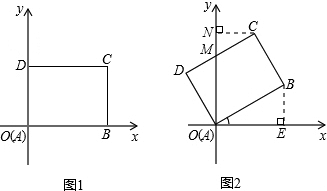
易知图1中点C的坐标为(4,3),
在图2中,设CD与y轴交于点M,作CN⊥y轴于点N,那么∠DOM=30°,OD=3,
∴DM=3•tan30°= ,OM=3÷cos30°=2
,OM=3÷cos30°=2 ,
,
那么CM=4- ,易知∠NCM=30°,
,易知∠NCM=30°,
∴MN=CM•sin30°= ,CN=CM•cos30°=
,CN=CM•cos30°=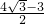 ,
,
则ON=OM+MN=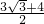 ,
,
∴图2中C点的坐标为(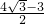 ,
,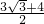 ).
).
点评:旋转前后对应角的度数不变,对应线段的长度不变,注意构造直角三角形求解.
 ,2) (4,3)(
,2) (4,3)(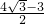 ,
,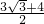 )
)分析:根据旋转的性质求解.
旋转的性质是旋转不改变图形的大小和形状.
解答:∵AB=4,在x轴正半轴上,
∴图1中B坐标为(4,0),
在图2中过B作BE⊥x轴于点E,那么OE=4×cos30°=2
 ,BE=2,
,BE=2,在图2中B点的坐标为(2
 ,2);
,2);
易知图1中点C的坐标为(4,3),
在图2中,设CD与y轴交于点M,作CN⊥y轴于点N,那么∠DOM=30°,OD=3,
∴DM=3•tan30°=
 ,OM=3÷cos30°=2
,OM=3÷cos30°=2 ,
,那么CM=4-
 ,易知∠NCM=30°,
,易知∠NCM=30°,∴MN=CM•sin30°=
 ,CN=CM•cos30°=
,CN=CM•cos30°=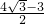 ,
,则ON=OM+MN=
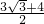 ,
,∴图2中C点的坐标为(
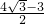 ,
,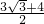 ).
).点评:旋转前后对应角的度数不变,对应线段的长度不变,注意构造直角三角形求解.

练习册系列答案
相关题目
 已知抛物线y=ax2-2x+c与它的对称轴相交于点A(1,-4),与y轴交于C,与x轴正半轴交于B.
已知抛物线y=ax2-2x+c与它的对称轴相交于点A(1,-4),与y轴交于C,与x轴正半轴交于B.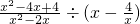 ,然后从-
,然后从- <x<
<x< 某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3米,探测线与地面的夹角分别是30°和60°(如图),试确定生命所在点C的深度.(结果保留根号)
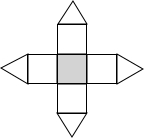
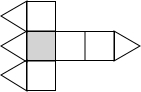
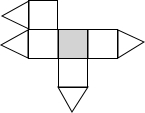
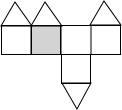
某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3米,探测线与地面的夹角分别是30°和60°(如图),试确定生命所在点C的深度.(结果保留根号)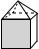 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是
如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是