ЬтФПФкШн
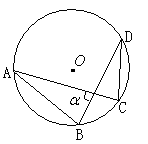
ЁОЬтФПЁПШчЭМЃЌвд ![]() ЮЊдЕуЕФжБНЧзјБъЯЕжаЃЌ
ЮЊдЕуЕФжБНЧзјБъЯЕжаЃЌ ![]() ЕуЕФзјБъЮЊЃЈ0ЃЌ 1ЃЉЃЌжБЯп
ЕуЕФзјБъЮЊЃЈ0ЃЌ 1ЃЉЃЌжБЯп ![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЖЏЕуЃЌзїжБЯп
ЩЯвЛЖЏЕуЃЌзїжБЯп![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ Й§
ЃЎ Й§![]() ЕузїжБЯп
ЕузїжБЯп![]() ЦНаагк
ЦНаагк![]() жсЃЌНЛ
жсЃЌНЛ![]() жсгкЕу
жсгкЕу ![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБЕу![]() дкЕквЛЯѓЯоЪБЃЌЧѓжЄЃК
дкЕквЛЯѓЯоЪБЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБЕу![]() дкЕквЛЯѓЯоЪБЃЌЩш
дкЕквЛЯѓЯоЪБЃЌЩш![]() ГЄЮЊ
ГЄЮЊ![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧыЧѓГі
ЃЌЧыЧѓГі![]() гы
гы![]() МфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСП
МфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯвЦЖЏЪБЃЌЕу
ЩЯвЦЖЏЪБЃЌЕу![]() вВЫцжЎдкжБЯп
вВЫцжЎдкжБЯп![]() ЩЯвЦЖЏЃЌ
ЩЯвЦЖЏЃЌ![]() ЪЧЗёПЩФмГЩЮЊЕШбќШ§НЧаЮЃПШчЙћПЩФмЃЌЧѓГіЫљгаФмЪЙ
ЪЧЗёПЩФмГЩЮЊЕШбќШ§НЧаЮЃПШчЙћПЩФмЃЌЧѓГіЫљгаФмЪЙ![]() ГЩЮЊЕШбќжБНЧШ§НЧаЮЕФЕу
ГЩЮЊЕШбќжБНЧШ§НЧаЮЕФЕу![]() ЕФзјБъЃЛШчЙћВЛПЩФмЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШчЙћВЛПЩФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉS=![]() m2Љ
m2Љ![]() m+1ЃЈ0ЃМmЃМ
m+1ЃЈ0ЃМmЃМ![]() ЃЉЃЛЃЈ3ЃЉЪЙЁїPBCГЩЮЊЕШбќШ§НЧаЮЕФЕуPЕФзјБъЮЊЃЈ0ЃЌ1ЃЉЛђЃЈ
ЃЉЃЛЃЈ3ЃЉЪЙЁїPBCГЩЮЊЕШбќШ§НЧаЮЕФЕуPЕФзјБъЮЊЃЈ0ЃЌ1ЃЉЛђЃЈ![]() ЃЌ1Љ
ЃЌ1Љ![]() ЃЉ.
ЃЉ.
ЁОНтЮіЁП
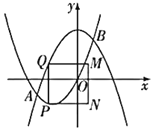
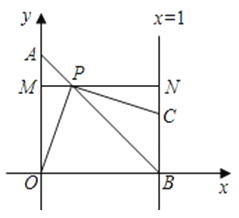
ЃЈ1ЃЉгЩЬтвтПЩЕУЁїOABЮЊЕШбќжБНЧШ§НЧаЮЃЌвђЮЊMNЁЮOBЃЌвзЕУЁїAMPвВЪЧЕШбќжБНЧШ§НЧаЮЃЌНјЖјПЩЕУOM=PNЃЌдйИљОнЁЯOPC=90ЁуЃЌЭЌНЧЕФгрНЧЯрЕШПЩЕУЁЯMOP=ЁЯNPCЃЌдђЭЈЙ§ЁАНЧБпНЧЁБМДПЩЕУжЄЃЛ
ЃЈ2ЃЉЩш![]() ГЄЮЊ
ГЄЮЊ![]() ЃЌИљОнЬтвтПЩгУmБэЪОГіAMЁЂMPЁЂOMЕШЕФГЄЃЌдйИљОнS=SОиOBNMЉ2SЁїPOMМДПЩЕУЕНSгыmЕФКЏЪ§ЙиЯЕЪНЃЌШЛКѓИљОнCдйЕквЛЯѓЯоЃЌЕУГіCNЕФШЁжЕЗЖЮЇЃЌНјЖјЕУЕНmЕФШЁжЕЗЖЮЇЃЛ
ЃЌИљОнЬтвтПЩгУmБэЪОГіAMЁЂMPЁЂOMЕШЕФГЄЃЌдйИљОнS=SОиOBNMЉ2SЁїPOMМДПЩЕУЕНSгыmЕФКЏЪ§ЙиЯЕЪНЃЌШЛКѓИљОнCдйЕквЛЯѓЯоЃЌЕУГіCNЕФШЁжЕЗЖЮЇЃЌНјЖјЕУЕНmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіНјааЬжТлЃКЕБCдкЕквЛЯѓЯоЪБЃЌвЊЪЙЁїPCBЮЊЕШбќШ§НЧаЮЃЌФЧУДPC=CBЃЌЁЯPBC=45ЁуЃЌДЫЪБPгыAжиКЯЃЌдђПЩЕУPЕузјБъЃЛЕБCдкЕкЫФЯѓЯоЪБЃЌPB=BCЃЌдкЕШбќжБНЧШ§НЧаЮPBNжаЃЌгУmБэЪОГіBPЕФГЄЃЌНјЖјЕУЕНBCЕФГЄЃЌгЩЃЈ1ЃЉПЩЕУMP=NCЃЌдђПЩСаГіЙигкmЕФЗНГЬЃЌЧѓЕУmЕФжЕЃЌНјЖјЕУЕНPЕузјБъ.
ЃЈ1ЃЉЁпOMЁЮBNЃЌMNЁЮOBЃЌЁЯAOB=90ЁуЃЌ
ЁрЫФБпаЮOBNMЮЊОиаЮЃЌ
ЁрMN=OB=1ЃЌЁЯPMO=ЁЯCNP=90ЁуЃЌ
ЁпOA=OBЃЌ
ЁрЁЯOAB=ЁЯOBA=45ЁуЃЌ
ЁрЁЯAPM=ЁЯABO=45ЁуЃЌ
ЁрЁЯMAP=ЁЯMPA=45ЁуЃЌ
ЁрAM=PMЃЌ
ЁрOM=AOЉAMЃЌPN=OBЉPMЃЌМДOM=PNЃЌ
гжЁпЁЯOPC=90ЁуЃЌ
ЁрЁЯMPO+ЁЯNPC=90ЁуЃЌ
ЁпЁЯMPO+ЁЯMOP=90ЁуЃЌ
ЁрЁЯMOP=ЁЯNPCЃЌ
Ёр![]() ЃЈASAЃЉЃЛ
ЃЈASAЃЉЃЛ
ЃЈ2ЃЉЩш![]() ГЄЮЊ
ГЄЮЊ![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ
ЁпAM=PM=APsin45Ёу=![]() mЃЌ
mЃЌ
ЁрOM=1Љ![]() mЃЌ
mЃЌ
ЁрS=SОиOBNMЉ2SЁїPOM=ЃЈ1Љ![]() mЃЉЉ2ЁС
mЃЉЉ2ЁС![]() ЃЈ1Љ
ЃЈ1Љ![]() mЃЉЁЄ
mЃЉЁЄ![]() m
m
=![]() m2Љ
m2Љ![]() m+1ЃЈ0ЃМmЃМ
m+1ЃЈ0ЃМmЃМ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЁїPBCПЩФмЮЊЕШбќШ§НЧаЮ.
ЂйЕБPгыAжиКЯЪБЃЌPC=BC=1ЃЌДЫЪБPЃЈ0ЃЌ1ЃЉЃЛ
ЂкЕБCдкЕкЫФЯѓЯоЃЌЧвPB=CBЪБЃЌгаBN=PN=1Љ![]() mЃЌ
mЃЌ
ЁрBC=PN=![]() PN=
PN=![]() ЉmЃЌ
ЉmЃЌ
ЁрNC=BN+BC=1Љ![]() m+
m+![]() ЉmЃЌ
ЉmЃЌ
гЩЃЈ1ЃЉПЩЕУЃКNC=PM=![]() mЃЌ
mЃЌ
Ёр1Љ![]() m+
m+![]() Љm=
Љm=![]() mЃЌ
mЃЌ
НтЕУm=1ЃЌ
ЁрPM=![]() ЃЌBN=1Љ
ЃЌBN=1Љ![]() ЃЌ
ЃЌ
ЁрPЃЈ![]() ЃЌ1Љ
ЃЌ1Љ![]() ЃЉЃЛ
ЃЉЃЛ
гЩЬтвтПЩжЊPC=PBВЛГЩСЂЃЌ
дђЪЙЁїPBCГЩЮЊЕШбќШ§НЧаЮЕФЕуPЕФзјБъЮЊЃЈ0ЃЌ1ЃЉЛђЃЈ![]() ЃЌ1Љ
ЃЌ1Љ![]() ЃЉ.
ЃЉ.

 аЁВЉЪПЦкФЉДГЙи100ЗжЯЕСаД№АИ
аЁВЉЪПЦкФЉДГЙи100ЗжЯЕСаД№АИ УћаЃУћЪІХргХзївЕБОМгКЫаФЪдОэЯЕСаД№АИ
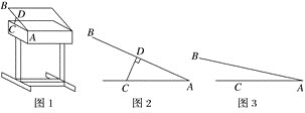
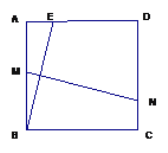
УћаЃУћЪІХргХзївЕБОМгКЫаФЪдОэЯЕСаД№АИЁОЬтФПЁПШчЭМЃЌQЪЧЛЁABгыЯвABЫљЮЇГЩЕФЭМаЮЕФФкВПЕФвЛЖЈЕуЃЌPЪЧЯвABЩЯвЛЖЏЕуЃЌСЌНгPQВЂбгГЄНЛЛЁABгкЕуCЃЌСЌНгBCЃЎвбжЊABЃН6cmЃЌЩшAЃЌPСНЕуМфЕФОрРыЮЊxcmЃЌPЃЌCСНЕуМфЕФОрРыЮЊy1cmЃЌAЃЌCСНЕуМфЕФОрРыЮЊy2cmЃЎ
аЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЗжБ№ЖдКЏЪ§y1ЃЌy2ЃЌЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉШЗЖЈздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ЃЈ2ЃЉАДЯТБэжаздБфСПxЕФжЕНјааШЁЕуЁЂЛЭМЁЂВтСПЃЌЗжБ№ЕУЕНСЫy1ЃЌy2гыxЕФМИзщЖдгІжЕЃЎ
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.62 | 4.67 | 3.76 | 2.65 | 3.18 | 4.37 | |
y2/cm | 5.62 | 5.59 | 5.53 | 5.42 | 5.19 | 4.73 | 4.11 |
ЃЈ3ЃЉдкЭЌвЛЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіВЙШЋКѓЕФБэжаИїзщЪ§жЕЫљЖдгІЕФЕуЃЈxЃЌy1ЃЉЃЌЃЈxЃЌy2ЃЉЃЌВЂУцГіКЏЪ§y1ЃЌy2ЕФЭМЯѓЃЎ
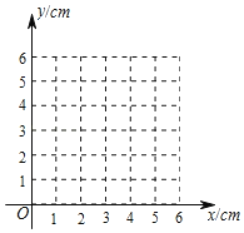
ЃЈ4ЃЉНсКЯКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБЁїAPCЮЊЕШбќШ§НЧаЮЪБЃЌAPЕФГЄЖШдМЮЊ cmЃЎ