Question

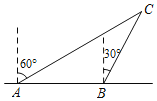
【题目】如图所示，一艘轮船在近海处由西向东航行，点C处有一灯塔，灯塔附近30海里的圆形区域内有暗礁，轮船在A处测得灯塔在北偏东60°方向上，轮船又由A向东航行40海里到B处，测得灯塔在北偏东30°方向上．

（1）求轮船在B处时到灯塔C处的距离是多少？

（2）若轮船继续向东航行，有无触礁危险？

Answer 1

【答案】(1)40海里；（2）轮船继续向东航行，无触礁危险．

【解析】

（1）根据三角形内角和定理求出∠ACB，根据等腰三角形的判定定理解答；

（2）作CE⊥AB交AB的延长线于E，根据正弦的定义求出CE，比较得到答案．

（1）由题意得，∠CAB=30°，∠ABC=120°，

∴∠ACB=180°-30°-120°=30°，

∴∠ACB=∠CAB，

∴BC=AB=40（海里）；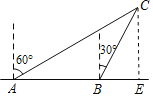

（2）作CE⊥AB交AB的延长线于E，

在Rt△CBE中，sin∠CBE=，

∴CE=BCsin∠CBE=40×=20，

∵20＞30，

∴轮船继续向东航行，无触礁危险．