Question

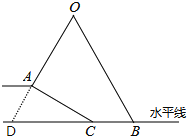
【题目】小明坐于堤边垂钓，如图，河堤AC的坡角为30°，AC长2，钓竿AO的倾斜角∠ODC是60°，其长OA为5米，若AO与钓鱼线OB的夹角为60°，求浮漂B与河堤下端C之间的距离．

Answer 1

【答案】浮漂B与河堤下端C之间的距离为3米．

【解析】

试题分析：先根据三角形内角和定理求出∠CAD=180°﹣∠ODB﹣∠ACD=90°，解Rt△ACD，得出AD=ACtan∠ACD=2米，CD=2AD=3米，再证明△BOD是等边三角形，得到BD=OD=OA+AD=7米，然后根据BC=BD﹣CD即可求出浮漂B与河堤下端C之间的距离．

解：∵AO的倾斜角是60°，

∴∠ODB=60°．

∵∠ACD=30°，

∴∠CAD=180°﹣∠ODB﹣∠ACD=90°．

在Rt△ACD中，AD=ACtan∠ACD=2×=2（米），

∴CD=2AD=4米，

又∵∠O=60°，

∴△BOD是等边三角形，

∴BD=OD=OA+AD=2+5=7（米），

∴BC=BD﹣CD=7﹣4=3（米）．

答：浮漂B与河堤下端C之间的距离为3米．