题目内容
【题目】如图，已知抛物线y=ax2+bx+c经过A （1，0）、B（0，3）及C（3，0）点，动点D从原点O开始沿OB方向以每秒1个单位长度移动，动点E从点C开始沿CO方向以每秒1个长度单位移动，动点D、E同时出发，当动点E到达原点O时，点D、E停止运动．
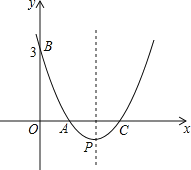
（1）求抛物线的解析式及顶点P的坐标；
（2）若F（﹣1，0），求△DEF的面积S与E点运动时间t的函数解析式；当t为何值时，△DEF的面积最大？最大面积是多少？
（3）当△DEF的面积最大时，抛物线的对称轴上是否存在一点N，使△EBN是直角三角形？若存在，求出N点的坐标，若不存在，请说明理由．
【答案】（1）y=x2﹣4x+3，（2，﹣1）；（2）当t=2时，S最大=2；（3）N点的坐标（2，2），（2，1），（2，
），（2，
）．
【解析】
试题分析：（1）根据待定系数法，可得函数解析式，根据配方法，可得顶点坐标；
（2）根据三角形的面积公式，可得函数解析式，根据二次函数的性质，可得答案；
（3）根据勾股定理的逆定理，可得关于a的方程，根据解方程，可得N点坐标．
解：（1）将A （1，0）、B（0，3）及C（3，0）代入函数解析式，得
，
解得
，
抛物线的解析式为y=x2﹣4x+3，
配方，得y=（x﹣2）2﹣1，顶点P的坐标为（2，﹣1）；
（2）如图1
，
由题意，得
CE=t，OE=3﹣t，FE=4﹣t，OD=t．
S=
FEOD=（4﹣t）t=﹣t2+2t=﹣
（t﹣2）2+2，
当t=2时，S最大=2；
（3）当△DEF的面积最大时，E（1，0），设N（2，a），
BN2=4+（a﹣3）2，EN2=1+a2，BE2=1+9=10，
①当BN2+EN2=BE2时，4+9﹣6a+a2+a2+1=10，化简，得
a2﹣3a+2=0，解得a=2，a=1，N（2，2），N（2，1）；
②当BN2+BE2=EN2时，4+9﹣6a+a2+10=1+a2，化简，得
6a=22，解得a=，N（2，）；
③当BE2+EN2=BN2时，1+a2+10=4+9﹣6a+a2，
化简，得
6a=2，解得a=，N（2，），
综上所述：N点的坐标（2，2），（2，1），（2，），（2，）．
