题目内容
【题目】如图，利用热气球探测器测量大楼AB的高度，从热气球P处测得大楼B的俯角为37°，大楼底部A的俯角为60°，此时热气球P离底面的高度为120m．试求大楼AB的高度（结果保留整数）．
（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， 
≈1.73）
【答案】解：如图，过点P作PC⊥AB，垂足为点C，
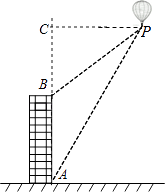
∵热气球P离底面的高度为120m，
∴AC=120m．
由题意知，∠APC=60°，∠BPC=37°，
∵tan∠APC= 
，即tan60°= 
，PC= 
=40 
；
在Rt△BPC中，由tan∠BPC= 
得，BC=PCtan37°=40 ×tan37°，
∴AB=AC﹣BC=120﹣40 tan37°≈120﹣40×1.73×0.75=68.1≈68（m）．
答：大楼AB的高度为68米．
【解析】解直角三角形可把特殊角放在直角三角形中，须作垂线，构造直角三角形，利用三角函数由边求边.
练习册系列答案
阅读快车系列答案
相关题目
