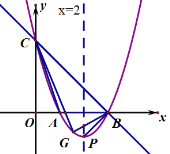
题目内容
【题目】如图![]() 中
中![]() ,
,![]() ,D、E为BC上两点,且
,D、E为BC上两点,且![]() .将
.将![]() 绕A顺时针旋转90°得到
绕A顺时针旋转90°得到![]() ,连接EF,下列结论:①AE平分
,连接EF,下列结论:①AE平分![]() ②
②![]() ③
③![]() ④
④![]() ,正确的有(序号)______.
,正确的有(序号)______.

【答案】①②③
【解析】
由△ADC绕点A顺时针旋转90°得△AFB,可知△ADC≌△AFB,∠FAD=90°,由∠DAE=45°可判断∠FAE=∠DAE,可证△AED≌△AEF.由已知条件可证△BEF为直角三角形,则有BE2+DC2=DE2是正确的.
解:∵△ADC绕点A顺时针旋转90°得△AFB,
∴△ADC≌△AFB,∠FAD=90°,
∴AD=AF,
∵∠DAE=45°,
∴∠FAE=90°-∠DAE=45°,
∴∠DAE=∠FAE,
∴AE平分![]() ,故①正确;
,故①正确;
在△AED与△AEF中,
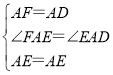
∴△AED≌△AEF(SAS),故②正确;
∴ED=FE,∠ACB=∠ABF,
在Rt△ABC中,
∵∠ABC+∠ACB=90°,
∴∠ABC+∠ABF=90°即∠FBE=90°,
∴BE2+BF2=FE2,即BE2+DC2=DE2,故③正确;
∵∠ABC=45°,设![]()
∴∠BEF=45°
∵∠FBE=90°
∴∠BFE=45°
∴BF=BE
∴DC=BE
又∵D、E为BC上两点
∴BE不一定等于DC,即④错误.
故答案为:①②③.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目