题目内容
【题目】P是⊙O外一点，PA、PB分别与⊙O相切于点A、B，点C是劣弧AB上任意一点，经过点C作⊙O的切线，分别交PA、PB于点D、E．若PA=4，则△PDE的周长是（ ）
A.4
B.8
C.12
D.不能确定
【答案】B
【解析】解：根据题意画出图形，如图所示，
由直线DA和直线DC为圆O的切线，得到AD=DC，同理，由直线EC和直线EB为圆O的切线，得到EC=EB，
又直线PA和直线PB为圆O的切线，所以PA=PB=4，
则△PDE的周长C=PD+DE+PE=PD+DC+EC+PE
=PD+DA+EB+PE=PA+PB=4+4=8．
故选B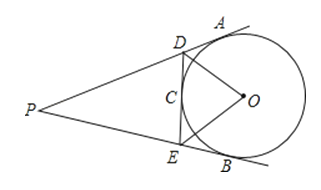
【考点精析】通过灵活运用切线的性质定理，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
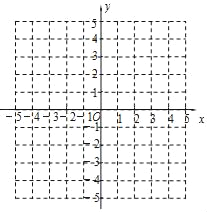
【题目】请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质，并解决问题．
(1)完成下列步骤，画出函数y=|x|的图象；
①列表、填空；
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 1 | 1 | 2 | 3 | … |
②描点；
③连线．
(2)观察图象，当x 时，y随x的增大而增大；
(3)根据图象，不等式|x|＜
x+
的解集为 ．
