题目内容
【题目】已知：如图，⊙O是△ABC的内切圆，下列说法错误的是（ ）
A.点O在△ABC的三边垂直平分线上
B.点O在△ABC的三个内角平分线上
C.如果△ABC的面积为S，三边长为a，b，c，⊙O的半径为r，那么r=
D.如果△ABC的三边长分别为5，7，8，那么以A、B、C为端点三条切线长分别为5，3，2
【答案】A
【解析】解：∵⊙O是△ABC的内切圆，
∴点O到△ABC三边的距离相等，
∴点O在△ABC的三个内角平分线上，故A错误，B正确，
连接OA，OB，OC，
∴S=S△ABO+S△BCO+S△ACO=
cr+arbr=（a+b+c）r，
∴r=
， 故C正确，
设以A、B、C为端点三条切线长分别为：x，y，z，
则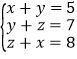
，
解得：
，
故D正确，
故选A．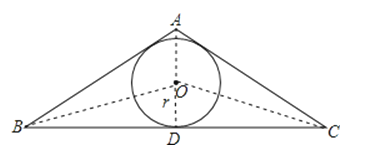
【考点精析】认真审题，首先需要了解三角形的内切圆与内心(三角形的内切圆的圆心是三角形的三条内角平分线的交点，它叫做三角形的内心)．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
