Question

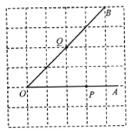
【题目】已知：如图，在直角坐标系中，⊙O1经过坐标原点，分别与x轴正半轴、y轴正半轴交于点A（3，0）、B（0，4）．设△BOA的内切圆的直径为d，求d+AB的值．

Answer 1

【答案】解：设△BOA的内切圆与OA、OB、AB分别切于点D、E、F，且半径为x．
∵∠AOB=90°，OA=3，0B=4，
∴AB=5．
∴OD=OE=x，BE=BF=4﹣x，AD=AF=3﹣x．
∴（4﹣x）+（3﹣x）=5．
解得x=1．
∴d+AB=2+5=7．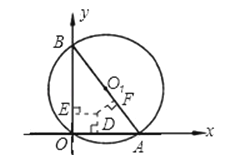

【解析】根据勾股定理求得斜边AB的长，再根据直角三角形的内切圆的半径等于两条直角边的和与斜边的差的一半，进一步计算其内切圆的直径，从而求得结果．
【考点精析】解答此题的关键在于理解三角形的内切圆与内心的相关知识，掌握三角形的内切圆的圆心是三角形的三条内角平分线的交点，它叫做三角形的内心．