题目内容
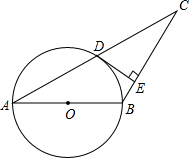
如图，⊙O的圆心在Rt△ABC的直角边AC上，⊙O经过C、D两点，与斜边AB交于点E
，连接BO、ED，有BO∥ED，作弦EF⊥AC于G，连接DF．
（1）求证：AB为⊙O的切线；
（2）若⊙O的半径为5，sin∠DFE=
，求EF的长．
，连接BO、ED，有BO∥ED，作弦EF⊥AC于G，连接DF．（1）求证：AB为⊙O的切线；
（2）若⊙O的半径为5，sin∠DFE=
| 3 |
| 5 |
（1）证明：连接OE．
∵ED∥OB，
∴∠1=∠2，∠3=∠OED．
又OE=OD，
∴∠2=∠OED，
∴∠1=∠3．
又OB=OB，OE=OC，
∴△BCO≌△BEO．（SAS）
∴∠BEO=∠BCO=90°，即OE⊥AB．
∴AB是⊙O切线．
（2）连接CE，
∵∠F=∠4，CD=2•OC=10；
由于CD为⊙O的直径，∴在Rt△CDE中有：
ED=CD•sin∠4=CD•sin∠DFE=10×
=6．
∴CE=
=
=8．
在Rt△CEG中，
=sin∠4=
，
∴EG=
×8=
．
根据垂径定理得：EF=2EG=
．
∵ED∥OB，
∴∠1=∠2，∠3=∠OED．
又OE=OD，
∴∠2=∠OED，
∴∠1=∠3．
又OB=OB，OE=OC，
∴△BCO≌△BEO．（SAS）
∴∠BEO=∠BCO=90°，即OE⊥AB．
∴AB是⊙O切线．
（2）连接CE，
∵∠F=∠4，CD=2•OC=10；
由于CD为⊙O的直径，∴在Rt△CDE中有：
ED=CD•sin∠4=CD•sin∠DFE=10×
| 3 |
| 5 |
∴CE=
| CD2-ED2 |
| 102-62 |
在Rt△CEG中，
| EG |
| CE |
| 3 |
| 5 |
∴EG=
| 3 |
| 5 |
| 24 |
| 5 |
根据垂径定理得：EF=2EG=
| 48 |
| 5 |
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
于点E．
