题目内容
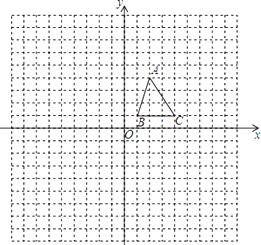
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数y=![]() (x>0)的图象经过点D,已知S△BCE=2,则k的值是_____.
(x>0)的图象经过点D,已知S△BCE=2,则k的值是_____.
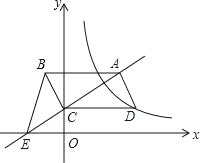
【答案】4.
【解析】
过点D作DF⊥x轴于点F,设点D的坐标为(m,![]() )(m>0).由平行四边形的性质可得出BC=AD,再结合平行线的性质以及角的计算得出∠ECO=∠ADC,通过解直角三角形用∠ADC的余弦、m和k表示出BC和CE,由S△BCE=2结合三角形的面积公式即可得出关于k的一元一次方程,解方程即可得出结论;
)(m>0).由平行四边形的性质可得出BC=AD,再结合平行线的性质以及角的计算得出∠ECO=∠ADC,通过解直角三角形用∠ADC的余弦、m和k表示出BC和CE,由S△BCE=2结合三角形的面积公式即可得出关于k的一元一次方程,解方程即可得出结论;
解:过点D作DF⊥x轴于点F,如图所示.
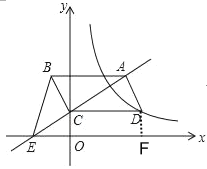
∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.
又∵BC⊥AC,
∴DA⊥AC,
∵CD平行于x轴,
∴∠ACD=∠CEO.
∵CO⊥OE,DA⊥AC,
∴∠ECO=∠ADC,
设点D的坐标为(m,![]() )(m>0),
)(m>0),
则CD=m,OC=DF=![]() ,
,
在Rt△CAD中,CD=m,∠CAD=90°,AD=mcos∠ADC,
在Rt△COE中,OC=![]() ,∠COE=90°,CE=
,∠COE=90°,CE=![]() =
=![]() ,
,
∴S△BCE=![]() CEBC=
CEBC=![]() ·
·![]() mcos∠ADC=
mcos∠ADC=![]() k=2,
k=2,
解得:k=4,
故答案为:4.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目