题目内容
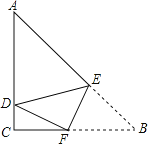
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=2.动点P以每秒2个单位长度的速度从点A出发,沿A→C→B的方向向终点B运动(点P不与△ABC的顶点重合).点P关于点C的对称点为点D,过点P作PQ⊥AB于点Q,以PD、PQ为边作□PDEQ.设□PDEQ与△ABC.重叠部分的面积为S,点P的运动时间为t(s)

(1)当点P在AC上运动时,用含t的代数式表示PD的长;
(2)当点E落在△ABC的直角边上时,求t的值;
(3)当□PDEQ与△ABC重叠部分的图形是四边形时,求S与t之间的函数关系式.
【答案】(1)4-4t;(2)![]() 或
或![]() ;(3)
;(3)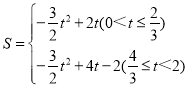
【解析】
(1)由题意得AP=2t,得到PC=2-2t,再根据对称性即可求解;
(2)根据题意作图分情况讨论,利用三角函数及三角形的关系即可列式求解;
(3)根据题意分情况讨论,利用割补法即可求解.
(1)∵AC=2,由题意得AP=2t,
∴PC=2-2t,
∵P、D关于C对称,
∴PD=2PC=4-4t;
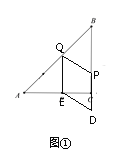
(2)如图①,当P在BC边上时,PC=2t-2,∴PD=4t-4,
∵四边形PDEQ为平行四边形,
∴QE=PD=4t-4,QE∥PD,
∵∠ACB=90°,AC=BC=2,
∴∠A=∠B=45°,∠QEA=90°,
∴AQ=![]() =
=![]() (4t-4)
(4t-4)
∵BC=2,∴BP=4-2t,
∴QB=BP·cos45°=![]() (2-t)
(2-t)
∵AB=![]()
∴AQ+QB=![]() (4t-4)+
(4t-4)+![]() (2-t)=2
(2-t)=2![]()
解得t=![]() ;
;
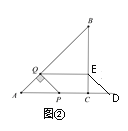
如图②,当P在AD边上时,由(1)得PD=4-4t,
∴QE=PD=4-4t,
∵∠B=45°,
QB=![]() (4-4t)
(4-4t)
∵AP=2t,
∴AQ=![]() t,
t,
∵AB=2![]()
∴![]() t+
t+![]() (4-4t)=2
(4-4t)=2![]()
解得t=![]() ;
;
综上,t=![]() 或
或![]() ;
;
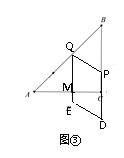
(3)如图③,由(2)得当![]() ,P在BC上时,设QE与AC交于M,
,P在BC上时,设QE与AC交于M,
∵PC=2t-2,
∴BP=2-(2t-2)=4-2t,
∴BQ=![]() (2-t)
(2-t)
∴AQ=AB-QB=2![]() -
-![]() (2-t)=
(2-t)=![]() t
t
∴AM=AQ·cos45°=t,
∴S△AMQ=![]() ,S△BQP=
,S△BQP=![]() BQ×QP=4-4t+
BQ×QP=4-4t+![]() ,
,
∴S四边形QMCP= S△ACB- S△AMQ- S△BQP=![]() ;
;
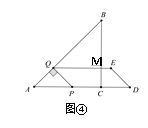
如图④,当![]() 时,P在AC上时,设QE与BC交于M,
时,P在AC上时,设QE与BC交于M,
∵AQ=![]() t
t
∴BQ=2![]() -
-![]() t
t
∴BM=BQ·cos45°=2-t,
∴S△QMB=![]() ,S△AQP=
,S△AQP=![]() ,
,
∴S四边形QMCP= S△ACB- S△QMB- S△AQP=![]()
综上,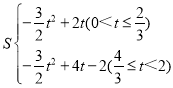 ,
,

 名校课堂系列答案
名校课堂系列答案