题目内容
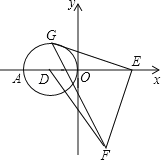
【题目】△ABC在平面直角坐标系中的位置如图所示:
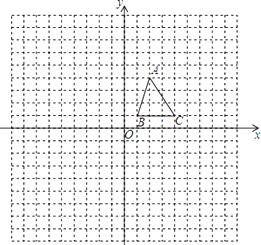
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在y轴左侧将△A1B1C1放大为原来的2倍,得到△A2B2C2,请画出△A2B2C2;
(3)设P(x,y)为△ABC内任意一点,△A2B2C2内的点P′是点P经过上述两次变换后的对应点,请直接写出P′的坐标___________.
【答案】(1)见解析;(2)见解析;(3) P′(-2x , 2y)
【解析】
(1)根据关于x轴对称性质找到A1、B1、C1的位置,然后画出图形即可;
(2)分别连接A1、B1、C1和O,然后反向延长扩大2倍,分别得到A2、B2、C2的位置,再画出图形即可;
(3)根据关于x轴对称的性质及位似特点写出P′坐标即可.
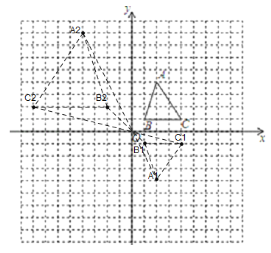
解:(1)根据关于x轴对称性质找到A1、B1、C1的位置,然后画出图形,如图△A1B1C1为所作;
(2)分别连接A1、B1、C1和O,然后反向延长扩大2倍,分别得到A2、B2、C2的位置,再画出图形,如图△A2B2C2为所作;
(3)根据关于x轴对称的性质得到变化坐标为(x,-y),以原点O为位似中心,在y轴左侧将△A1B1C1放大为原来的2倍得到P′的坐标为横纵坐标同时乘-2,即P′的坐标为(-2x,2y).

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目