Question

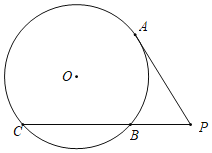
【题目】如图，PA为⊙O的切线，PB与⊙O交于B、C两点，已知PA＝6，PB＝3，则PC＝_____．

Answer 1

【答案】12

【解析】

连接AO并延长交⊙O于E，连接BE，AB，由切线的性质得到∠EAP＝90°，根据圆周角定理得到∠ABE＝90°，根据余角的性质和圆周角定理得到∠C＝∠PAB，根据相似三角形的性质即可得到结论．

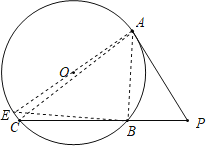
解：连接AO并延长交⊙O于E，连接BE，AB，

∵PA为⊙O的切线，

∴∠EAP＝90°，

∴∠EAB+∠PAB＝90°，

∵AE是⊙O的直径，

∴∠ABE＝90°，

∴∠E+∠EAB＝90°，

∴∠E＝∠BAP，

∵∠E＝∠C，

∴∠C＝∠PAB，

∵∠P＝∠P，

∴△APB∽△CPA，

∴，

∴＝，

∴PC＝12，

故答案为：12．