题目内容
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴、y轴上,反比例函数y= ![]() (x>0)的图像经过点D,且与边BC交于点E,则点E的坐标为.
(x>0)的图像经过点D,且与边BC交于点E,则点E的坐标为. 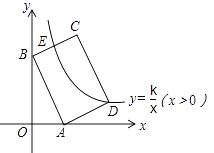
【答案】(2,7)
【解析】解:过点D作DF⊥x轴于点F,则∠AOB=∠DFA=90°,∴∠OAB+∠ABO=90°,
∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC,
∴∠OAB+∠DAF=90°,
∴∠ABO=∠DAF,
∴△AOB∽△DFA,
∴OA:DF=OB:AF=AB:AD,
∵AB:BC=3:2,点A(3,0),B(0,6),
∴AB:AD=3:2,OA=3,OB=6,
∴DF=2,AF=4,
∴OF=OA+AF=7,
∴点D的坐标为:(7,2),
∴反比例函数的解析式为:y= ![]() ①,点C的坐标为:(4,8),
①,点C的坐标为:(4,8),
设直线BC的解析式为:y=kx+b,
则 ![]() ,
,
解得: ![]()
∴直线BC的解析式为:y= ![]() x+6②,
x+6②,
联立①②得: ![]() 或
或 ![]() (舍去),
(舍去),
∴点E的坐标为:(2,7).
所以答案是:(2,7).

练习册系列答案
相关题目