题目内容
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的 ![]() O与边AB相交于点D,DE⊥AC,垂足为点E.
O与边AB相交于点D,DE⊥AC,垂足为点E. 
(1)求证:点D是AB的中点;
(2)判断DE与 ![]() O的位置关系,并证明你的结论;
O的位置关系,并证明你的结论;
(3)若 ![]() O的直径为3,cosB=
O的直径为3,cosB= ![]() ,求DE的长.
,求DE的长.
【答案】
(1)解:证明:连结CD,如图,
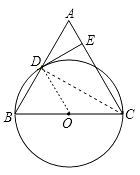
∵BC为直径,
∴∠BDC=90°,
∴CD⊥AB,
∵AC=BC,
∴AD=BD,
即点D是AB的中点;
(2)解:DE与⊙O相切.理由如下:
连结OD,
∵AD=BD,OC=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
而DE⊥AC,
∴DE⊥OD,
∴DE为⊙O的切线.
(3)解:连结CD,如图,
∵BC为直径,
∴∠BDC=90°,
在Rt△BDC中,∵cosB= ![]() ,
,
∴BD= ![]() BC=
BC= ![]() ×3=1,
×3=1,
∴AD=BD=1,
在Rt△ADE中,∵cosA=cosB= ![]() =
= ![]()
∴AE= ![]() AD=
AD= ![]() ,
,
∴DE= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)连结OD,如图,由OD=OB得到∠ODB=∠B,由CA=CB得到∠A=∠B,则∠ODB=∠A,则可判断OD∥AC,易得BD=AD,即点D是AB的中点;(2)由于OD∥AC,DE⊥AC,所以DE⊥OD,于是根据切线的判定定理可得DE为⊙O的切线;(3)连结CD,如图,根据圆周角定理得到∠BDC=90°,则在Rt△BDC中,利用余弦定义可计算出BD= ![]() BC=1,所以AD=BD=1,接着在Rt△ADE中,利用余弦定义可计算出AE=
BC=1,所以AD=BD=1,接着在Rt△ADE中,利用余弦定义可计算出AE= ![]() AD=
AD= ![]() ,然后根据勾股定理可计算出DE的长.
,然后根据勾股定理可计算出DE的长.
【考点精析】通过灵活运用切线的判定定理,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】为了解高邮市6000名九年级学生英语口语考试成绩的情况,从中随机抽取了部分学生的成绩(满分30分,得分均为整数),制成下表:
分数段(x分) | x≤10 | 11≤x≤15 | 16≤x≤20 | 21≤x≤25 | 26≤x≤30 |
人 数 | 10 | 15 | 35 | 112 | 128 |
(1)本次抽样调查共抽取了名学生;
(2)若用扇形统计图表示统计结果,则分数段为x≤10的人数所对应扇形的圆心角为°;
(3)学生英语口语考试成绩的众数落在11≤x≤15的分数段内;(填“会”或“不会”)
(4)若将26分以上(含26)定为优秀,请估计该区九年级考生成绩为优秀的人数.
【题目】用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元. 设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) | 0.5 | 2 | … | ||
乙复印店收费(元) | 0.6 | 2.4 | … |
(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1 , y2关于x的函数关系式;
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.