题目内容
【题目】![]() 与
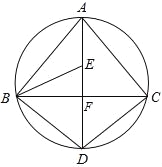
与 ![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.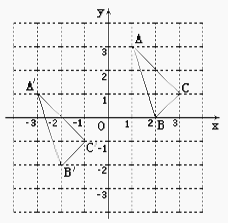
(1)分别写出下列各点的坐标:![]() ,
, ![]() ,
, ![]() ;
;
(2)说明 ![]() 由
由 ![]() 经过怎样的平移得到:;
经过怎样的平移得到:;
(3)若点 ![]() (
( ![]() ,
, ![]() )是
)是 ![]() 内部一点,则平移后
内部一点,则平移后 ![]() 内的对应点
内的对应点 ![]() 的坐标为;
的坐标为;
(4)求 ![]() 的面积.
的面积.
【答案】
(1)解:(-3,1);(-2,-2);(-1,-1)
(2)先向左平移4个单位,再向下平移2个单位或先向下平移2个单位,再向左平移4个单位。
(3)(a-4,b-2)
(4)
将 补成长方形,减去3个直角三角形的面积得:6-1.5-0.5-2=2.
【解析】分析:⑴根据网格确定点的坐标;⑵观察两个三角形一对对应点,如A与 ![]() ,再沿着网格左右、上下平移即可;⑶根据平移规律:横坐标左减右加,纵坐标下减上加;⑷用割补法求面积.
,再沿着网格左右、上下平移即可;⑶根据平移规律:横坐标左减右加,纵坐标下减上加;⑷用割补法求面积.
【考点精析】关于本题考查的三角形的面积和坐标与图形变化-平移,需要了解三角形的面积=1/2×底×高;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目