题目内容
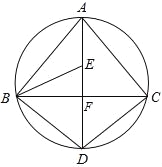
【题目】已知,如图,△ABC的三个顶点A,B,C在以AD直径的圆上,且AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)若∠BCD=∠BAD,请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
【答案】(1)证明见解析;
(2)B,E,C三点在以D为圆心,以DB为半径的圆上.
【解析】
试题分析:(1)利用等弧对等弦即可证明.
(2)利用等弧所对的圆周角相等,∠BAD=∠CBD再等量代换得出∠DBE=∠DEB,从而证明DB=DE=DC,所以B,E,C三点在以D为圆心,以DB为半径的圆上.
试题解析:(1)证明:∵AB是直径,AD⊥BC,
∴弧BD=弧CD,
∴BD=CD
(2)B,E,C三点在以D为圆心,以DB为半径的圆上.
理由:由(1)知:弧BD=弧CD,
∴∠BAD=∠CBD,
又∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE,∠CBE=∠ABE,
∴∠DBE=∠DEB,
∴DB=DE.
由(1)知:BD=CD
∴DB=DE=DC.
∴B,E,C三点在以D为圆心,以DB为半径的圆上.

练习册系列答案
相关题目