题目内容
【题目】（1）如图①，在矩形ABCD中，AB＝4，AD＝10，在BC边上是否存在点P，使∠APD＝90°，若存在，请用直尺和圆规作出点P并求出BP的长．（保留作图痕迹）
（2）如图②，在△ABC中，∠ABC＝60°，BC＝12，AD是BC边上的高，E、F分别为AB，AC的中点，当AD＝6时，BC边上是否存在一点Q，使∠EQF＝90°，求此时BQ的长．
【答案】（1）2或8；（2）存在，3+
.
【解析】试题分析：（1）以AD为直径画圆与BC交于点P1、P2，则点P1、P2为所求点；由矩形的性质得到AD=BC=10，AB=CD=4根据三角形相似即可解出；
（2）由三角形的中位线得到EF∥BC，EF=
BC=6，根据EF与BC间距离为3，推出以EF为直径的 O与BC相切，得出BC上符合条件的点Q只有一个，记 O与BC相切于点Q，连接OQ，过点E作EG⊥BC，垂足为G，证出四边形EOQG为正方形，由勾股定理即可求出．
解：（1）如图①所示，点P1、P2为所求的点；（保留作图痕迹）
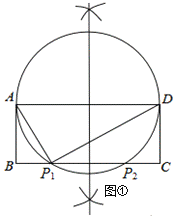
在矩形ABCD中，连接AP1、DP1，AD=BC=10，AB=CD=4，
设BP1=x，则P1C=10﹣x，
∵∠AP1D=90°，∴∠AP1B+∠CP1D=90°，
∵∠BAP1+∠AP1B=90°，∴∠BAP1=∠CP1D，
又∵∠B=∠C=90°，∴△ABP1∽△P1CD，
∴
，∴
，
解得：x1=2，x2=8，∴BP的长是2或8
（2）如图②，
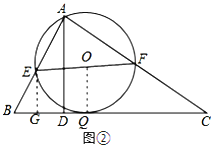
∵EF分别为AB、AC的中点，∴EF∥BC，EF=BC=6，
∵AD=6，AD⊥BC，∴EF与BC间距离为3，
∴以EF为直径的⊙O与BC相切，
∴BC上符合条件的点Q只有一个，记⊙O与BC相切于点Q，
连接OQ，过点E作EG⊥BC，垂足为G，
∴EG=OE=3，∴四边形EOQG为正方形，
在Rt△EBG中，∠B=60°，EG=3，∴BG=，∴BQ=3+．
