题目内容
【题目】已知:如图,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使锐角△AOB的面积等于3.求点B的坐标.

【答案】(1)y=x2-3x,(2)(4,4).
【解析】试题分析:(1)将原点坐标代入抛物线中即可求出k的值,也就得出了抛物线的解析式.
(2)根据(1)得出的抛物线的解析式可得出A点的坐标,也就求出了OA的长,根据△OAB的面积可求出B点纵坐标的绝对值,然后将符合题意的B点纵坐标代入抛物线的解析式中即可求出B点的坐标,然后根据B点在抛物线对称轴的右边来判断得出的B点是否符合要求即可.
试题解析:①∵函数的图象与x轴相交于O,
∴0=k+1,
∴k=-1,
∴y=x2-3x,
②假设存在点B,过点B做BD⊥x轴于点D,
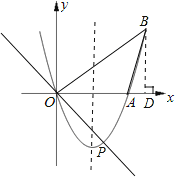
∵△AOB的面积等于6,
∴![]() AOBD=6,
AOBD=6,
当0=x2-3x,
x(x-3)=0,
解得:x=0或3,
∴AO=3,
∴BD=4
即4=x2-3x,
解得:x=4或x=-1(舍去).
又∵顶点坐标为:(1.5,-2.25).
∵2.25<4,
∴x轴下方不存在B点,
∴点B的坐标为:(4,4).

练习册系列答案
相关题目
【题目】如图1,在△ABC中,OB、OC是∠ABC、∠ACB的角平分线;
(1)填写下面的表格.
∠A的度数 | 50° | 60° | 70° |
∠BOC的度数 |
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想;
(3)如图2,△ABC的高BE、CD交于O点,试说明图中∠A与∠BOD的关系.