Question

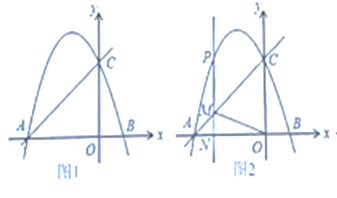
【题目】如图1．抛物线经过点点在抛物线上，且在轴的上方，点的横坐标记为．

（1）求抛物线的解析式：

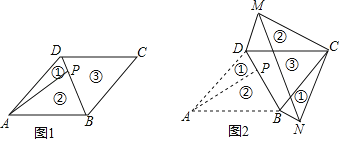
（2）如图2．过点作轴的平行线交直线于点．交轴于点，若平分，求的值：

（3）点在直线上．点在轴上，且位于点的上方，那么在抛物线上是否存在点，使得以点为顶点的四边形是菱形？若存在，请直接写出菱形的面积．

Answer 1

【答案】（1）；（2）；（3）存在，或

【解析】

（1）设抛物线的解析式为，将点C（0,3）代入即可解答；

（2）求出直线AC的解析式为，设P的横坐标为t，则，根据平行线的性质以及角平分线的定义得到，根据勾股定理列出方程即可求出t的值；

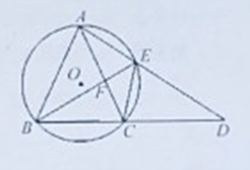
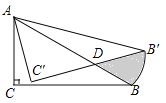
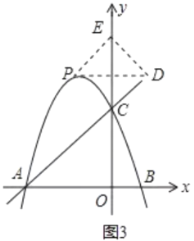
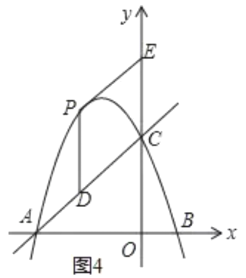
（3）分两种情况：①当CE为对角线时，四边形CPED为菱形，如图3，则点P和点D关于y轴对称；②当CE为菱形的边时，四边形CEPD为菱形，如图4，则PD∥y轴，CD=PD，分别构建方程即可解决问题．

解：（1）∵抛物线经过点，

∴设抛物线的解析式为，

把代入得到

抛物线的解析式为，

即

（2）如图2中

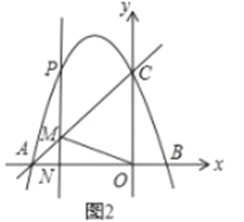
设直线AC的解析式为y=kx+p，将代入得：

，解得k=，p=3，

直线的解析式为

的横坐标为，

平分，

，

，

，

，解得或t=0（舍去）

的值为

（3）设，

①当CE为对角线时，四边形CPED为菱形，如图3，则点P和点D关于y轴对称，

∴点，

将代入中得：

，

解得：（舍去）

此时P（-2，），

∴PD=4，CE=2×（-3）=3

∴菱形的面积=；

②当CE为菱形的边时，四边形CEPD为菱形，如图4，则PD∥y轴，CD=PD，

∴，

∴PD=

而，

∴，

∴，解得：（舍去），

∴PD=，

此时菱形的面积=．

综上所述，菱形的面积是或．