题目内容
【题目】如图，在边长为1个单位长度的小正方形网格中建立平面直角坐标系，已知
的顶点
的坐标为
，顶点
的坐标为
，顶点
的坐标为
.
（1）求的面积；
（2）若把向上平移3个单位长度，再向左平移6个单位长度得到
，请画出；
（3）若点
在
轴上，且
的面积与的面积相等，请直接写出点的坐标.
【答案】（1）
；（2）见解析；（3）点
的坐标是
或
【解析】
（1）利用三角形面积公式计算；
（2）利用点平移的坐标变换规律写出A′、B′、C′的坐标，然后描点即可；
（3）设P（0，t），根据三角形面积公式得到
×3×|t+1|=，然后求出t即可得到P点坐标．
解：（1）
的面积等于
.
（2）画出的
如图所示：
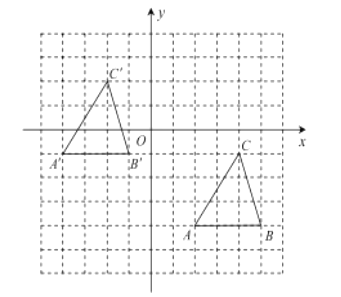
（3）设P（0，t），
∵△PA′B′的面积与△ABC的面积相等，
∴×3×|t+1|=，解得t=2或t=-4，
∴P点坐标为（0，2）或（0，-4）．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某校为了解学生参加“经典诵读”的活动情况.该校随机选取部分学生，对他们在三、四月份的诵读时间进行调查，下面是根据调查数据制作的统计图表的一部分.
四月份日人均诵读时间的统计表
日人均诵读时间 | 人数 | 百分比 |
| 6 | |
| 30 | |
|
|
|
| 10 |
|
|
|
|
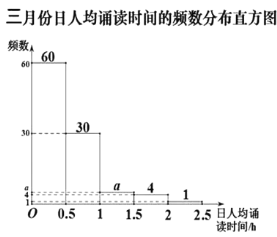
根据以上信息，解答下列问题：
（1）本次调查的学生人数为______；
（2）图表中的
，
，
，
的值分别为______，______，______，______；
（3）在被调查的学生中，四月份日人均诵读时间在
范围内的人数比三月份在此范围的人数多______人.
