题目内容
【题目】如图,直线CD与直线AB相交于C,根据下列语句画图,并填空.
(1)过点P作PQ∥CD,交AB于点Q(尺规作图);
(2)过点P作PR⊥CD,垂足为R.
(3)在(1)(2)的条件下,若∠ACD=65°,则∠PQB=____度,∠RPQ=____度.

【答案】(1)见详解;(2)见详解;(3)故答案为115,90.
【解析】
(1)平移CD使它经过点P即可得到PQ;
(2)过点P作PR⊥DC于R;
(3)先根据平行线的性质得∠PQA=∠ACD=65°,则利用邻补角计算∠PQB,根据垂直定义得∠PRC=90°,然后利用平行线的性质求∠RPQ=90°.
解:(1)如图,PQ为所作;
(2)如图,PR为所作;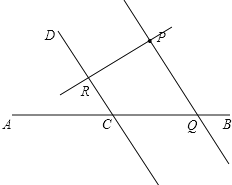
(3)在图中,∵PQ∥CD,
∴∠PQA=∠ACD=65°,
∴∠PQB=180°-65°=115°,
∵PR⊥CD,
∴∠PRC=90°,
∵PQ∥CD,
∴∠RPQ+∠PRC=180°,
∴∠RPQ=90°.
故答案为115,90.

练习册系列答案
相关题目