题目内容
(6分)在平面直角坐标系xOy中,二次函数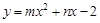 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.
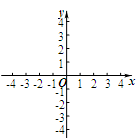
(1)求此二次函数的解析式;
(2)点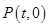 是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
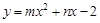 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.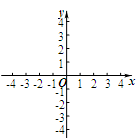
(1)求此二次函数的解析式;
(2)点
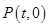 是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.(1)y=x2+x-2 (2)-1﹤t﹤1.
试题分析:求函数解析式的常用方法是待定系数法,由于已知给出了c的值,又知两个坐标点,所以代入即可求出a ,b的值。由于点P在x轴上,由图像知a﹥0,所以开口向上,因图像与x轴有两个交点,所以满足题意的横坐标t,只有在点A,B之间取得。解:(1)把A(-1,-2)、B(1,0)分别代入
 中,
中,∴
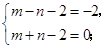 2分;
2分;解得:
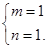 3分;
3分;∴所求二次函数的解析式为
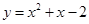 . 4分;
. 4分;(2)
 . 6分.
. 6分.点评:熟知二次函数的图像与性质,在解题过程中由已知可求的解析式,需要注意的是,在求取值范围时,要结合函数的图像。本题属于基础题,难度不大。

练习册系列答案
相关题目
 与x轴交A,B两点(A点在B点左侧),直线
与x轴交A,B两点(A点在B点左侧),直线 与抛物线交于A,C两点,其中C点的横坐标为2.
与抛物线交于A,C两点,其中C点的横坐标为2.
 轴的平行线交抛物线于E点,求线段PE长度的最大值;
轴的平行线交抛物线于E点,求线段PE长度的最大值; 过点A(-1,0),B(4,0),P(5,3),抛物线与y轴交于点C.
过点A(-1,0),B(4,0),P(5,3),抛物线与y轴交于点C.
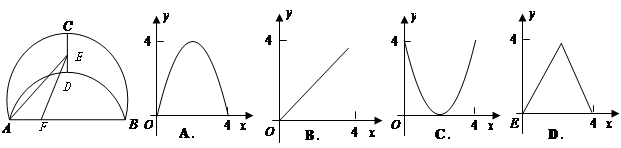
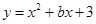 的对称轴为
的对称轴为 ,则
,则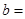 .
.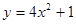

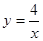
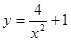
 向左平移2个单位后所得到的抛物线为( )
向左平移2个单位后所得到的抛物线为( )


