题目内容
【题目】某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
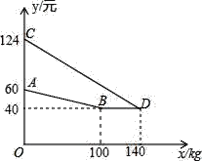
(1)请解释图中点D的实际意义.
(2)求线段CD所表示的y2与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
【答案】(1)点D的实际意义:当产量为140kg时,该产品每千克生产成本与销售价相等,都为40元;(2)y2=﹣![]() x+124(0≤x≤140); (3)当该产品的质量为80kg时,获得的利润最大,最大利润为2560元.
x+124(0≤x≤140); (3)当该产品的质量为80kg时,获得的利润最大,最大利润为2560元.
【解析】
(1)点D的横坐标、纵坐标的实际意义:当产量为140kg时,该产品每千克生产成本与销售价相等,都为40元.
(2)根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可.
(3)先求出销售价![]() 与产量x之间的函数关系,利用:总利润=每千克利润×产量列出有关x的一次函数,求得最值即可.
与产量x之间的函数关系,利用:总利润=每千克利润×产量列出有关x的一次函数,求得最值即可.
解:(1)点D的实际意义:当产量为140kg时,该产品每千克生产成本与销售价相等,都为40元.
(2)设线段CD所表示的y2与x之间的函数表达式为y2=k1x+b1,
∵点(0,124),(140,40)在函数y2=k1x+b1的图象上,
∴y2与x之间的函数表达式为y2=﹣![]() x+124(0≤x≤140);
x+124(0≤x≤140);
(3)设线段AB所表示的y1与x之间的函数表达式为y1=k2x+b2,
∵点(0,60),(100,40)在函数y1=k2x+b2的图象上,
∴y1与x之间的函数表达式为y1=﹣![]() x+60(0≤x≤100)
x+60(0≤x≤100)
设产量为x千克时,获得的利润为W元.
①当0≤x≤100时,W=[(﹣![]() x+124)﹣(﹣
x+124)﹣(﹣![]() x+60)]x=﹣
x+60)]x=﹣![]() (x﹣80)2+2560,
(x﹣80)2+2560,
∴当x=80时,W的值最大,最大值为2560元.
②当100≤x≤140时,W=[(﹣![]() x+124)﹣40]x=﹣
x+124)﹣40]x=﹣![]() (x﹣70)2+2940, 由﹣
(x﹣70)2+2940, 由﹣![]() <0知,
<0知,
当x≥70时,W随x的增大而减小,
∴当x=100时,W的值最大,最大值为2400元.
∵2560>2400,
∴当该产品的质量为80kg时,获得的利润最大,最大利润为2560元.

 阅读快车系列答案
阅读快车系列答案【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.