题目内容
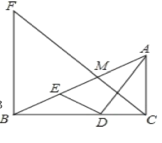
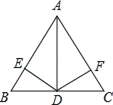
【题目】如图,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,则下列各式正确的是( )①AD2=BDDC;②CD2=CFCA;③DE2=AEAB;④AEAB=AFAC.
A.①②B.①③C.②④D.③④
【答案】C
【解析】
①式可变形为![]() ,采用三点定型法,可知需要证明△ADB与△CDA相似,但是明显无法证明,故①错误;
,采用三点定型法,可知需要证明△ADB与△CDA相似,但是明显无法证明,故①错误;
②式可变形为![]() ,采用三点定型法,可知需要△ADC∽△DFC相似,证明即可.
,采用三点定型法,可知需要△ADC∽△DFC相似,证明即可.
③式可变形为![]() ,采用三点定型法,可知需要△BED∽△DEA相似,证明即可.
,采用三点定型法,可知需要△BED∽△DEA相似,证明即可.
④式可变形为![]() ,采用三点定型法,可知需要△ABD∽△ADE相似,证明即可.
,采用三点定型法,可知需要△ABD∽△ADE相似,证明即可.
解:∵△ADB与△CDA不能确定相似,
∴不能确定![]() =
=![]() ,故①错误;
,故①错误;
∵∠ACD=∠DCF,∠ADC=∠DFC=90°,
∴△ADC∽△DFC,
∴![]() ,
,
∴CD2=CACF,故②正确;
∵∠BDE+∠ADE=∠B+∠BDE=90°,
∴∠B=∠ADE,
∵∠BED=∠DEA=90°,
∴△BED∽△DEA,
∴![]() ,
,
∴DE2=AEBE,故③错误;
∵∠EAD=∠DAB,∠AED=∠ADB=90°,
∴△ABD∽△ADE,
∴![]() ,
,
∴AD2=AEAB,
同理可证AD2=AFAC,
∴AEAB=AFAC,故④正确.
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目