题目内容
【题目】为了了解某县中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩（单位：分），根据成绩分成如下四个组：
，
，
，
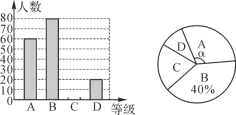
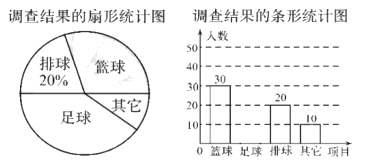
，并制作出如下的扇形统计图和频数分布直方图．
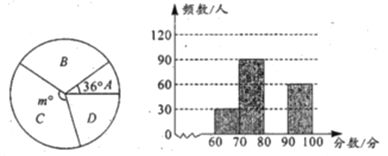
请根据图表中的信息，解答下列问题：
（1）扇形统计图中的
________，并补全频数分布直方图．
（2）4个小组每组推选1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中A，C两组学生的概率是多少？请列表或面树状图说明．
【答案】（1）144；补全频数分布直方图见解析；（2）P(恰好抽中A，C两组学生)
．
【解析】
（1）根据题意先利用A组的频数与它所占的百分比计算出调查的总人数，再计算出C组人数，然后用360乘以C组所占的百分比得到m的值，最后补全频数统计图即可；
（2）由题意通过列表展示所有12种等可能结果，再找出抽到A、C组人的结果数，然后根据概率公式求解．
解：（1）被抽查的学生一共有
（人），C组人数为
（人），
所以
，即
.
故答案为：144.
补全频数分布直方图如下：
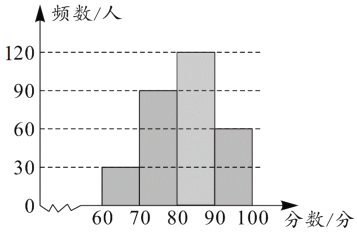
（2）列表如下：
第2人 第1人 | A | B | C | D |
A | A,B | A,C | A,D | |
B | B,A | B,C | B,C | |
C | C,A | C,B | C,D | |
D | D,A | D,B | D,C |
由表可知共有12种等可能结果，抽中A，C两组的共有 2 种结果，
∴P(恰好抽中A，C两组学生)
.
练习册系列答案
相关题目
