题目内容
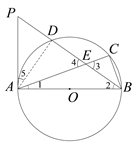
【题目】如图,AB是⊙O的直径,BC为弦,D为![]() 的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.
的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.

(1)求证:∠PAC=2∠CBE;
(2)若PD=m,∠CBE=α,请写出求线段CE长的思路.
【答案】(1)证明见解析; (2)思路见解析.
【解析】(1)证明:∵D为![]() 的中点
的中点
,
∴∠CBA=2∠CBE.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠1+∠CBA=90°.
∴∠1+2∠CBE =90°.
∵AP是⊙O的切线,
∴∠PAB=∠1+∠PAC=90°.
∴∠PAC =2∠CBE.
(2)思路:①连接AD,由D是![]() 的中点,∠2=∠CBE,
的中点,∠2=∠CBE,
由∠ACB=∠PAB=90°,得∠P=∠3=∠4,故AP=AE;
②由AB是⊙O的直径,可得∠ADB=90°;由AP=AE,
得PE=2PD=2m,∠5=![]() ∠PAC =∠CBE=
∠PAC =∠CBE= ![]()
③在Rt△PAD中,由PD=m,∠5= ![]() ,可求PA的长;
,可求PA的长;
④在Rt△PAB中,由PA的长和∠2= ![]() ,可求BP的长;
,可求BP的长;
由![]() 可求BE的长;
可求BE的长;
⑤在Rt△BCE中,由BE的长和![]() ,可求CE的长.
,可求CE的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目