题目内容
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

【答案】(1)![]() , D (
, D (![]() ,
,![]() );(2)△ABC是直角三角形,证明见解析;
);(2)△ABC是直角三角形,证明见解析;
(3)M(![]() ,0).
,0).
【解析】(1)∵点A(-1,0)在抛物线y=![]() x2 + bx-2上,
x2 + bx-2上,
∴![]() × (-1 )2 + b× (-1)–2 = 0,
× (-1 )2 + b× (-1)–2 = 0,
![]() 解得b =
解得b =![]() ,
,
∴ 抛物线的解析式为y=![]() x2-
x2-![]() x-2.
x-2.
y= ( x2 -3x- 4 ) =![]() (x-)2-
(x-)2-![]() ,
,
∴顶点D的坐标为 (![]() , -
, -![]() ).
).
(2)当x = 0时y = -2,
∴C(0,-2),OC = 2。
当y = 0时, ![]() x2-
x2-![]() x-2 = 0,
x-2 = 0,
∴x1 =-1, x2 = 4,
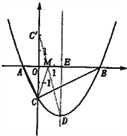
∴B (4,0)
∴OA = 1, OB = 4, AB = 5.
∵AB2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20,
∴AC2 +BC2 = AB2.
∴△ABC是直角三角形.
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC + MD的值最小及△DCM的周长最小
设抛物线的对称轴交x轴于点E.
∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴![]()
∴![]() , ∴m =
, ∴m =![]() .
.
所以M的坐标为(![]() ,0)
,0)

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目