题目内容
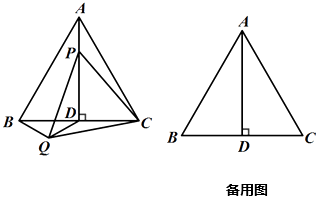
【题目】在锐角△ABC中,AB=AC,AD为BC边上的高,E为AC中点.
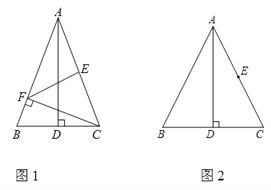
(1)如图1,过点C作CF⊥AB于F点,连接EF.若∠BAD=20°,求∠AFE的度数;
(2)若M为线段BD上的动点(点M与点D不重合),过点C作CN⊥AM于N点,射线EN,AB交于P点.
①依题意将图2补全;
②小宇通过观察、实验,提出猜想:在点M运动的过程中,始终有∠APE=2∠MAD.
小宇把这个猜想与同学们进行讨论,形成了证明该猜想的几种想法:
想法1:连接DE,要证∠APE=2∠MAD,只需证∠PED=2∠MAD.
想法2:设∠MAD=α,∠DAC=β,只需用α,β表示出∠PEC,通过角度计算得∠APE=2α.
想法3:在NE上取点Q,使∠NAQ=2∠MAD,要证∠APE=2∠MAD,只需证△NAQ∽△APQ.……
请你参考上面的想法,帮助小宇证明∠APE =2∠MAD.(一种方法即可)
【答案】(1)证明见解析;(2)① 补图见解析;②证明见解析.
【解析】(1)证明:∵AB=AC,AD为BC边上的高,∠BAD=20°,
∴∠BAC=2∠BAD=40°.
∵CF⊥AB, ∴∠AFC=90°.
∵E为AC中点,
∴EF=EA= ![]() .
.
∴∠AFE=∠BAC=40°.
(2)①
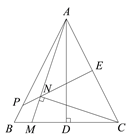
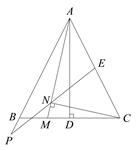
画出一种即可.
②证明:
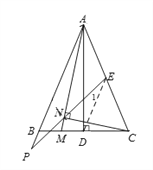
想法1:连接DE.
∵AB=AC,AD为BC边上的高,
∴D为BC中点.
∵E为AC中点,
∴ED∥AB,
∴∠1=∠APE.
∵∠ADC=90°,E为AC中点,
∴![]() .
.
同理可证![]() .
.
∴AE=NE=CE=DE.
∴A,N,D,C在以点E为圆心,AC为直径的圆上.
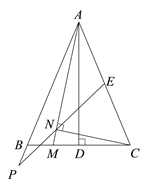
∴∠1=2∠MAD.
∴∠APE=2∠MAD.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目