题目内容
【题目】在平面直角坐标系xOy中,已知点A的坐标为(0,﹣1),点C(m,0)是x轴上的一个动点. 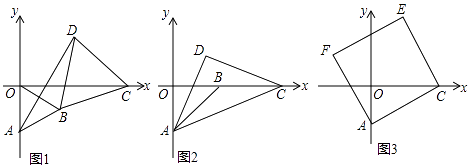
(1)如图1,点B在第四象限,△AOB和△BCD都是等边三角形,点D在BC的上方,当点C在x轴上运动到如图所示的位置时,连接AD,请证明△ABD≌△OBC;
(2)如图2,点B在x轴的正半轴上,△ABO和△ACD都是等腰直角三角形,点D在AC的上方,∠D=90°,当点C在x轴上运动(m>1)时,设点D的坐标为(x,y),请探求y与x之间的函数表达式;
(3)如图3,四边形ACEF是菱形,且∠ACE=90°,点E在AC的上方,当点C在x轴上运动(m>1)时,设点E的坐标为(x,y),请探求y与x之间的函数表达式.
【答案】
(1)解:∵△AOB和△BCD都是等边三角形,
∴AB=OB,BD=BC,∠ABO=∠DBC=60°,
∴∠ABD=∠OBC,
在△ABD和△OBC中,
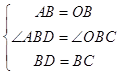 ,
,
∴△ABD和△OBC;
(2)解:如图,过点D作DH⊥y轴,垂足为H,延长HD,过点C作CG⊥HD,垂足为G.
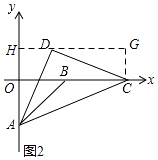
∴∠AHD=∠CGD=90°,
∵△ABO和△ACD都是等腰直角三角形,
∴∠ADC=90°,AD=CD,
∴∠ADH+∠CDG=90°,
∵∠ADH+∠DAH=90°,
∴∠CDG=∠DAH,
∵在△AHD和△DGC中,
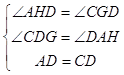 ,
,
∴△AHD≌△DGC(AAS),
∴DH=CG=OH,
∵点D的坐标为(x,y),
∴y与x之间的关系是y=x
(3)解:过点E作EM⊥x轴,垂足为M,则∠EMC=∠COA=90°,
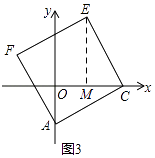
∵四边形ACEF是菱形,且∠ACE=90°,
∴AC=CE,∠ACO+∠ECO=90°,
∵∠ACO+∠CAO=90°,
∴∠ECO=∠CAO,
在△EMC和△COA中,
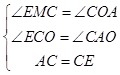 ,
,
∴△EMC≌△COA(AAS),
∴MC=OA=1,EM=OC,
∵点E的坐标为(x,y),
∴EM=OC=x+1,
∴y与x之间的关系是y=x+1.
【解析】(1.)由等边三角形的性质得到AB=OB,BD=BC,∠ABO=∠DBC=60°,从而判断出∠ABD=∠OBC即可; (2.)过点D作DH⊥y轴,垂足为H,延长HD,过点C作CG⊥HD,垂足为G,由△ABO和△ACD都是等腰直角三角形,得出∠ADC=90°,AD=CD,∠CDG=∠DAH,从而得到△AHD≌△DGC(AAS),根据DH=CG=OH,点D的坐标为(x,y),得出y与x之间的关系是y=x;
(3.)过点E作EM⊥x轴,垂足为M,则∠EMC=∠COA=90°,再利用正方形的性质即可得出△EMC≌△COA(AAS),得到MC=OA=1,EM=OC,EM=OC=x+1,进而得出y与x之间的关系是y=x+1.
【考点精析】根据题目的已知条件,利用等腰直角三角形和等边三角形的性质的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;等边三角形的三个角都相等并且每个角都是60°.