题目内容
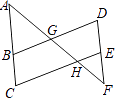
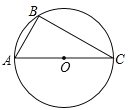
【题目】如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°.
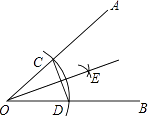
(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求△ABE与△CDE的面积之比.
【答案】(1)作图见试题解析;(2)![]() .
.
【解析】
试题分析:(1)①以点B为圆心,以任意长为半径画弧,两弧交角ABC两边于点M,N;②分别以点M,N为圆心,以大于![]() MN的长度为半径画弧,两弧交于一点;③作射线BE交AC与E,交⊙O于点D,则线段BD为△ABC的角平分线;
MN的长度为半径画弧,两弧交于一点;③作射线BE交AC与E,交⊙O于点D,则线段BD为△ABC的角平分线;
(2)连接OD,设⊙O的半径为r,可证△ABE∽△DCE,在Rt△ACB中,∠ABC=90°,∠ACB=30°,得到AB=![]() AC=r,得出△ADC是等腰直角三角形,在Rt△ODC中,得出DC=
AC=r,得出△ADC是等腰直角三角形,在Rt△ODC中,得出DC=![]() =
=![]() ,由相似三角形面积比等于相似比的平方即可得到结论.
,由相似三角形面积比等于相似比的平方即可得到结论.
试题解析:(1)如图所示;
(2)如图2,连接OD,设⊙O的半径为r,∵∠BAE=∠CDE,∠AEB=∠DEC,∴△ABE∽△DCE,在Rt△ACB中,∠ABC=90°,∠ACB=30°,∴AB=![]() AC=r,∵∠ABD=∠ACD=45°,∵OD=OC,∴∠ABD=∠ACD=45°,∴∠DOC=90°,在Rt△ODC中,DC=
AC=r,∵∠ABD=∠ACD=45°,∵OD=OC,∴∠ABD=∠ACD=45°,∴∠DOC=90°,在Rt△ODC中,DC=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() .
.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目