题目内容
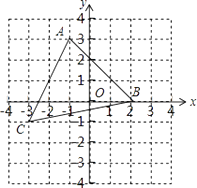
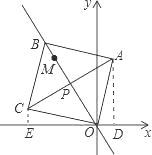
【题目】如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )

A. (![]() ,
, ![]() ) B. (
) B. (![]() ,11) C. (2,2
,11) C. (2,2![]() ) D. (
) D. (![]() ,
, ![]() )
)
【答案】B
【解析】试题解析:作AD⊥x轴于D,CE⊥x轴于E,
设直线OM的解析式为y=kx,
∵点M(-3,4),
∴4=-3k,
∴k=-![]() ,
,
∵四边形ABCO是正方形,
∴直线AC⊥直线OM,
∴直线AC的斜率为![]() ,
,
∵四边形ABCO是正方形,
∴OA=OC,∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°
∴∠COE=∠OAD,
在△COE和△OAD中,
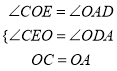
∴△COE≌△OAD(AAS),
∴CE=OD,OE=AD,
设A(a,b),则C(-b,a),
设直线AC的解析式为y=mx+n,
∴![]()
解得m=![]() ,
,
∴![]() ,
,
整理得,b=7a,
∵正方形面积为128,
∴OA2=128,
在RT△AOD中,AD2+OD2=OA2,即(7a)2+a2=128,
解得,a=![]() ,
,
∴b=7a=7×![]() =
=![]() ,
,
∴A(![]() ,
, ![]() ),
),
故选D.

练习册系列答案
相关题目