题目内容
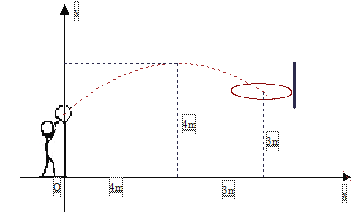
【题目】初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
【答案】(1)能够投中,理由见解析;(2)能够盖帽拦截成功.
【解析】试题分析:
(1)由题意可知抛物线经过(0, ![]() ),顶点坐标是(4,4),因此设抛物线的解析式为“顶点式”,代入两点坐标即可求得解析式;然后将篮圈的横坐标7代入解析式看对应的函数值是否等于篮圈的纵坐标即可判断能否投中;
),顶点坐标是(4,4),因此设抛物线的解析式为“顶点式”,代入两点坐标即可求得解析式;然后将篮圈的横坐标7代入解析式看对应的函数值是否等于篮圈的纵坐标即可判断能否投中;
(2)由题意将![]() 代入(1)中所求的解析式,看计算出的函数值是否小于或等于3.1,即可判断能否拦截成功.
代入(1)中所求的解析式,看计算出的函数值是否小于或等于3.1,即可判断能否拦截成功.
试题解析:
由题意可知,抛物线经过(0, ![]() ),顶点坐标是(4,4).
),顶点坐标是(4,4).
∴可设抛物线的解析式是![]() ,
,
代入点(0, ![]() ),得:
),得: ![]() ,解得
,解得![]() ,
,
∴抛物线的解析式是![]() ;
;
∵当![]() 时,
时, ![]() ,
,
∴代表篮圈的点(7,3)在抛物线上,
∴能够投中.
(2)∵当![]() 时,
时, ![]() <3.1,
<3.1,
∴乙能够盖帽拦截成功.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?