��Ŀ����
����Ŀ����ͼ����֪������y��ax2��bx��c��x�ύ��A��B���㣬��y�ύ�ڵ�C�� DΪOC���е㣬ֱ��AD���������ڵ�E��2��6��������ABE����ABC�����֮��Ϊ3��2��

��1�������������߶�Ӧ�ĺ�����ϵʽ��
��2������BD�����ж�BD��AD��λ�ù�ϵ����˵�����ɣ�
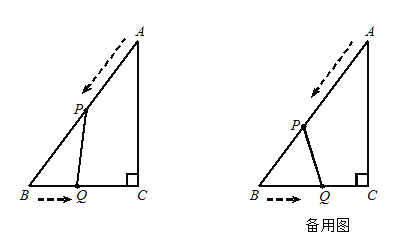
��3������BC��ֱ��AD�ڵ�M����ֱ��AD�ϣ��Ƿ���������ĵ�N�������M�غϣ���ʹ����A��B��NΪ���������������ABM���ƣ������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��������ABE����ABC�����֮��Ϊ3��2��E��2��6�����ɵ�C��0��4��.
��D��0��2��. ��D��0��2����E��2��6���ɵ�ֱ��AD����Ӧ�ĺ�����ϵʽΪy��2x��2.
��y��0ʱ��2x��2��0�����x����1. ��A����1��0��.
��A����1��0����C��0��4����E��2��6����������߶�Ӧ�ĺ�����ϵʽΪ
y����x2��3x��4.
��2��BD��AD.
���B��4��0����ͨ�����ƻɶ����涨��֤����BDA��90������BD��AD.
��3����1�����M��������AM��. ����ANB�ס�ABM����������AB2��AM��AN��
��52����AN�����AN��3.�Ӷ����N��2��6��.
��2����OB��OC��4����BOC��90������ABC��45��.
��BD��AD��BD��DE��2����AEB��45��.
���AEB�ס�ABM������E������������N��2��6��.
����������1��������ABE����ABC�����֮��Ϊ3��2��E��2��6�����ɵ�C��0��4��.
��D��0��2��. ��D��0��2����E��2��6�����ݴ���ϵ�����ɵ�ֱ��AD����Ӧ�ĺ�����ϵʽΪy��2x��2.
���һ�κ�����x��Ľ�������A����1��0������A����1��0����C��0��4����E��2��6�����ݴ���ϵ����
��������߶�Ӧ�ĺ�����ϵʽΪy����x2��3x��4.
���B��4��0����ͨ�����ƻɶ����涨��֤����BDA��90������BD��AD.
����ANB�ס�ABM�����ݶ�Ӧ�߳ɱ���������õ�N�����ꡣ