题目内容
【题目】如图,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=70°,分别求:
(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
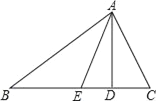
【答案】(1)80°;(2)70°;(3)20°.
【解析】
(1)根据三角形的内角和即可得到结论;
(2)根据角平分线的定义和三角形的内角和即可得到结论;
(3)根据极品飞车的定义和三角形的内角和即可得到结论.
(1)∵∠B=30°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
(2)∵AD为高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=90°﹣70°=20°,
而AE为角平分线,
∴∠CAE=![]() ∠BAC=40°,
∠BAC=40°,
∴∠AED=90°﹣(∠CAE﹣∠CAD)=90°﹣(40°﹣20°)=70°;
(3)∵AE是△ABC的角平分线,
∴∠BAE=![]() ∠BAC=40°,
∠BAC=40°,
又∵AD⊥BC,
∴∠BAD=90°﹣∠B=60°,
∴∠EAD=∠BAD﹣∠BAE=60°﹣40°=20°.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格﹣每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.