��Ŀ����
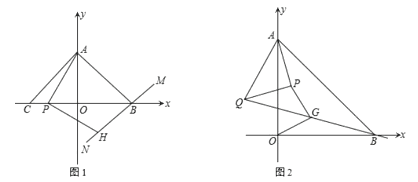
����Ŀ����ͼ��������A��B�����Ӧ���������ֱ�ΪxA����5��xB��6������P�ӵ�A��������ÿ��1����λ���ٶ���������A��B֮�������˶���ͬʱ����Q�ӵ�B��������ÿ��2����λ���ٶ���������B��A֮�������˶������˶�ʱ��Ϊt�룮
(1)��t��2ʱ����P��Ӧ��������xP��______��PQ��______��
(2)��0��t��11ʱ����ԭ��Oǡ�����߶�PQ���е㣬��t��ֵ��
(3)���ǰ������ϵ�������Ӧ�ĵ��Ϊ�����㡱����P��Q�����һ�������㴦�غ�ʱ��ֱ��д���������Ӧ������
![]()
���𰸡�(1)��3��5��(2)t��1��7��(3)6.
��������
��1�������P,Q��Ӧ����������PQ��ֵ����2���������ٵ�0��t��5.5ʱ����Q�˶���δ����A����AP��t��BQ��2t����ʱOP��|5��t|��OQ��|6��2t|���ڵ�5.5��t��11ʱ����P��������ԭ���Ҳ࣬��Q�Ѿ�������BA�����˶�����A���۷���Ҫʹԭ��Oǡ�����߶�PQ���е㣬��Q����λ��ԭ��O��ࣻ�г���Ӧ���̼��ɣ���3��������������t: �ٵ�0��t��5.5ʱ����Q�˶���δ����A����P��Q�����غ�ʱ��P��Q�������ڵ�5.5��t��11ʱ����P��������ԭ���Ҳ࣬��Q�Ѿ�������BA�����˶�����A���۷�����P��Q�����غ�ʱ����Q�ϵ�P��AQ��AP.
�⣺(1)��t��2ʱ����P��Ӧ��������xP����5+1��2����3��
��Q��Ӧ��������xQ��6��2��2��2��
��PQ��2��(��3)��5��
�ʴ�Ϊ��3��5��
(2)��xA����5��xB��6��
��OA��5��OB��6��
�������֪����0��t��11ʱ����P�˶�����Զ·��Ϊ�����ϴӵ�A����B����Q�˶�����Զ·��Ϊ�����ϴӵ�B����A�����۷��ص���B��
���ڵ�P����Ϊ�����˶��ٶ�vP��1����P�ӵ�A�˶�����O��Ҫ5�룬�˶�����B��Ҫ11�룮
���ڵ�Q����Ϊ�����˶��ٶ�vQ��2����Q�ӵ�B�˶�����O��Ҫ3�룬�˶�����A��Ҫ5.5�룬���ص���B��Ҫ11�룮
Ҫʹԭ��Oǡ�����߶�PQ���е㣬��ҪP��Q����ֱ���ԭ��O�����࣬��OP��OQ����ʱt��5.5��
�ٵ�0��t��5.5ʱ����Q�˶���δ����A����AP��t��BQ��2t��
��ʱOP��|5��t|��OQ��|6��2t|��
��ԭ��Oǡ�����߶�PQ���е㣬
��OP��OQ��
��|5��t|��|6��2t|��
���t��1��t��![]() ��
��
���飺��t��![]() ʱ��P��Q�����غϣ��Ҷ���ԭ��O��࣬����������ȥ��t��1�������⣮
ʱ��P��Q�����غϣ��Ҷ���ԭ��O��࣬����������ȥ��t��1�������⣮
��t��1��
�ڵ�5.5��t��11ʱ����P��������ԭ���Ҳ࣬��Q�Ѿ�������BA�����˶�����A���۷���Ҫʹԭ��Oǡ�����߶�PQ���е㣬��Q����λ��ԭ��O��࣬��ʱP��Q����Ĵ���λ������ͼ��ʾ��
![]()
��ʱ��OP��AP��OA��t��5��OQ��OA��AQ��5��2(t��5.5)��16��2t��
��ԭ��Oǡ�����߶�PQ���е㣬
��OP��OQ��
��t��5��16��2t��
���t��7��
���飺��t��7ʱ�������⣮
��t��7��
���Ͽ�֪��t��1��7��
(3)�ٵ�0��t��5.5ʱ����Q�˶���δ����A����P��Q�����غ�ʱ��P��Q��������ʱ��Ҫ��ʱ��Ϊ��![]() �룬
�룬
�������Ӧ����Ϊ��5+![]() ����
����![]() ���������㣬����������ȥ��
���������㣬����������ȥ��
�ڵ�5.5��t��11ʱ����P��������ԭ���Ҳ࣬��Q�Ѿ�������BA�����˶�����A���۷�����P��Q�����غ�ʱ����Q�ϵ�P��AQ��AP��
2(t��5.5)��t�����t��11��
�����Ӧ����Ϊ��5+11��6��
�ʵ�P��Q�����һ�������㴦�غ�ʱ���������Ӧ����Ϊ6��