题目内容
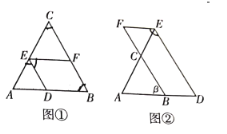
【题目】探究:如图①,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() ,
,![]() 上,且
上,且![]() ,
,![]() ∥
∥![]() ,若
,若![]() ,求
,求![]() 的度数.请把下面的解答过程补充完整.(请在空上填写推理依据或数学式子)
的度数.请把下面的解答过程补充完整.(请在空上填写推理依据或数学式子)
解:∵![]()
∴![]() ∥
∥![]() (_____________________________)
(_____________________________)
∴![]() ____________(_______________________)
____________(_______________________)
∵![]() ∥
∥![]()
∴_________![]() (_____________________)
(_____________________)
∴![]()
∵![]()
∴![]() _____________
_____________
应用:如图②,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() ,
,![]() 的延长线上,且
的延长线上,且![]() ,
,![]() ∥
∥![]() ,若
,若![]() ,则
,则![]() 的大小为_____________(用含
的大小为_____________(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)同位角相等,两直线平行;∠CFE;两直线平行,内错角相等;∠CFE;两直线平行,同位角相等; 65°;(2)180°-β
【解析】
探究:依据同位角相等,两直线平行,两直线平行,内错角相等以及两直线平行,同位角相等,即可得到∠DEF=∠ABC,进而得出∠DEF的度数.
应用:依据同位角相等,两直线平行以及两直线平行,同旁内角互补,即可得到∠DEF的度数.
解:∵![]()
∴![]() ∥
∥![]() (同位角相等,两直线平行)
(同位角相等,两直线平行)
∴∠DEF=(∠CFE)(两直线平行,内错角相等)
∵![]() ∥
∥![]()
∴(∠CFE)=∠ABC(两直线平行,同位角相等)
∴![]()
∵![]()
∴∠DEF=65°
故答案为:同位角相等,两直线平行;∠CFE;两直线平行,内错角相等;∠CFE;两直线平行,同位角相等; 65°.
应用:∵![]()
∴DE∥BC
∴∠ABC=∠D=β
∵EF∥AB
∴∠D+∠DEF=180°
∴∠DEF=180°-∠D=180°-β,
故答案为:180°-β.

练习册系列答案
相关题目